What is Pi? We celebrate “Pi Day” on March 14, so Pi is a mathematical idea that has its own day. That is good, because astronomy involves a lot of mathematical ideas. But still, what is Pi, and how do we know that?
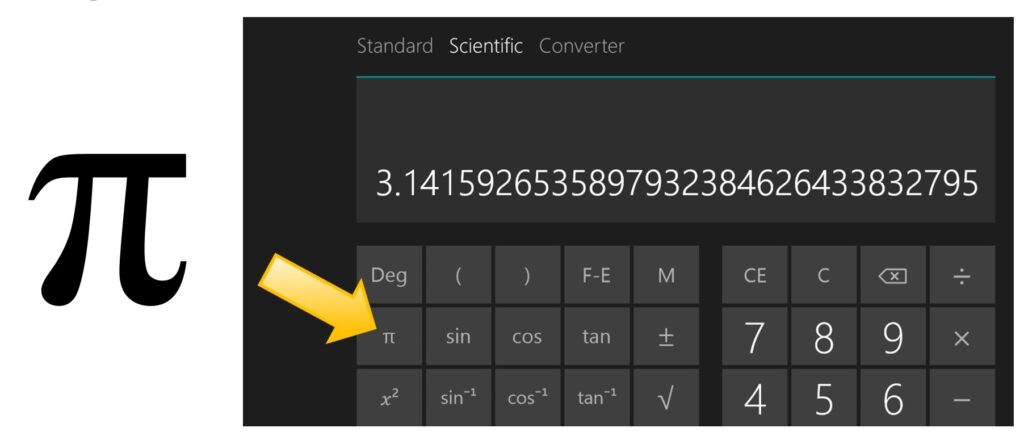
This question started bugging me after I bought my current laptop. For some reason the calculator “app” on this laptop is striking in a way that older calculator apps are not. Perhaps this is because the new app is large and bold. But at any rate, note how the button for π (that is, Pi) on the calculator app, when pressed, returns quite a long string of digits—3.1415926535897932384626433832795. That is thirty-two digits of Pi! Wow!
This bold string of digits raises the question: How do we know Pi to that many digits? Despite being a physicist, astronomer, and historian of science, despite using Pi all the time, despite teaching many students to use it regularly, I had only a vague idea how the value 3.1415926535897932384626433832795 might be obtained. So, I decided to figure this out, both because I should know, and because I thought a write-up on this would make a good hallway poster for the Science Building at Jefferson Community & Technical College in Louisville, Kentucky, where I am a professor. Math is a big stumbling block for JCTC students. At the college we are always looking for ways to advise students toward truly engaging the subject of mathematics, rather than viewing it as an onerous and pointless hoop (placed before them by the Authorities of Education) that they must simply jump through on the way to their degrees. But Pi is something everyone has heard about; it has its own Day, after all. This post then is based on that little JCTC poster project about what Pi is and how to determine its value for yourself.
Now you, O Reader, may view math no more positively than does the typical JCTC student. Maybe you do; you are reading an astronomy blog, after all. But plenty of people who like astronomy still care little for math, and think it to be beyond them. Indeed math is often portrayed as beyond the understanding of even the best-educated. But hang in there with this post, despite the counter-cultural implications implicit in reading stuff about math. Pi is cool. Mathematical reasoning is cool. And moving beyond just liking astronomy, and toward understanding how it works and how people over time have been able to figure out so much about the universe, is very cool.
So, if you wanted to figure out the value of Pi for yourself—if you wanted to make Homemade Pi, so to speak—you might just measure a round thing and calculate the value. Suppose you go find a nice sphere: a basketball. The ball’s Circumference C you could measure by wrapping a tape measure around the ball; its Diameter D you could measure by putting the ball between a couple of blocks. Since the Diameter D is twice the Radius R, the formula C=2πR that relates Circumference to Radius is also C=πD. You can calculate Pi by dividing the ball’s Circumference C by its Diameter D: π=C/D.
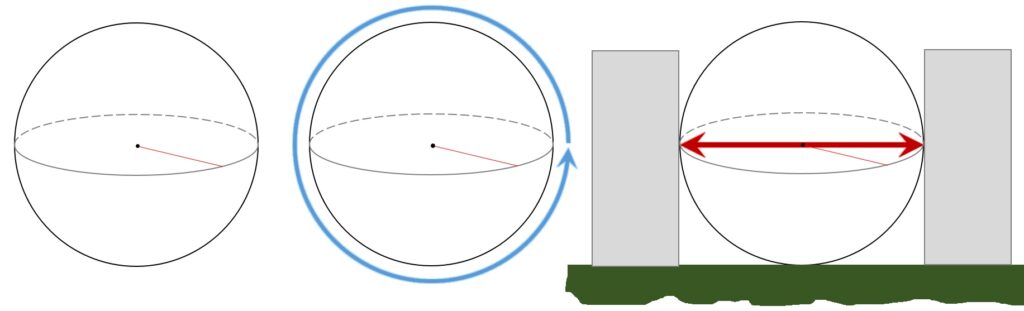 Left—a ball; middle—measuring the circumference of the ball; right—measuring the diameter of the ball.
Left—a ball; middle—measuring the circumference of the ball; right—measuring the diameter of the ball.Of course, that basketball might not be truly round. So suppose you could borrow one of the 1 kg silicon spheres made by the Australian Centre for Precision Optics. If you measured one of those you would be using something that qualifies as “the roundest object in the world.”
You use your tape measure and other paraphernalia to measure the Circumference and Diameter of the ACPO sphere. The smallest division on a tape measure is usually 1/16 inch (or 1/16”). Let’s imagine that you can determine Circumference and Diameter to half of one of those divisions, or 1/32”. With the tape measure you might find the Diameter of the sphere to be D=3 & 22/32”, which is 3.6875” in decimal form. You measure the Circumference to be C=11 & 18/32”, or 11.5625”. And now you proceed to calculate Pi from your measurements:
π=C/D=11.5625/3.6875=3.135593…
Obviously this only gets you a few digits of Pi!
So, you upgrade the equipment, getting some precision measurement tools from a machine shop. These let you measure to the nearest thousandth of an inch. Using these, you might find D=3.685”, C=11.577”. Again you proceed to calculate Pi from your measurements:
π=C/D=11.577/3.685=3.1416553…
Still not great!
Finally, suppose you could actually measure the ACPO sphere by counting individual atoms. According to ACPO, the spacing of individual atoms in the sphere is 0.9 nanometers, or a few hundred-millionths of an inch. This is the highest precision possible in measuring this roundest object in the world, because the object is made up of individual atoms; you will not find a half or a tenth or a hundredth of an atom in the sphere. At the single-atom level of precision you might get D=3.68503937”, C=11.57689261”, and
π=C/D=11.57689261/3.68503937=3.141592652780…
So, even if you could count individual atoms in the roundest object in the world, you could not determine Pi to even half the thirty-two digits given by the calculator app. And any achievable measurement of a normal round object, even at machine-shop-level precision, will only give Pi to a handful of digits.
Yet Pi has been determined to far more than thirty-two digits. The Pi Day web site will give a million digits of Pi, and it says that Pi has been calculated to a trillion digits! Clearly, the value of Pi is not found through measurement. If you want to make that Homemade Pi, you will have to use pure reason, not measurement. Reason can take you further than experimentation and measurement can go—as much further as a trillion is beyond thirty-two.
And that will be the subject of the next Pi post!