Sirius A & B, seen through the Hubble Space Telescope. The arrowed object is Sirius B.The brightest star* in the sky, Sirius, the Dog Star, was the subject of a nice, short article in the March 2020 issue of Sky & Telescope magazine. The article noted that Sirius is a double star: the Sirius that we point to in the night sky (what astronomers call “Sirius A”) is orbited by a faint companion star (“Sirius B”). Sirius B is most difficult to see through a telescope, owing to the brightness of Sirius A—but it can be spotted, and even photographed.
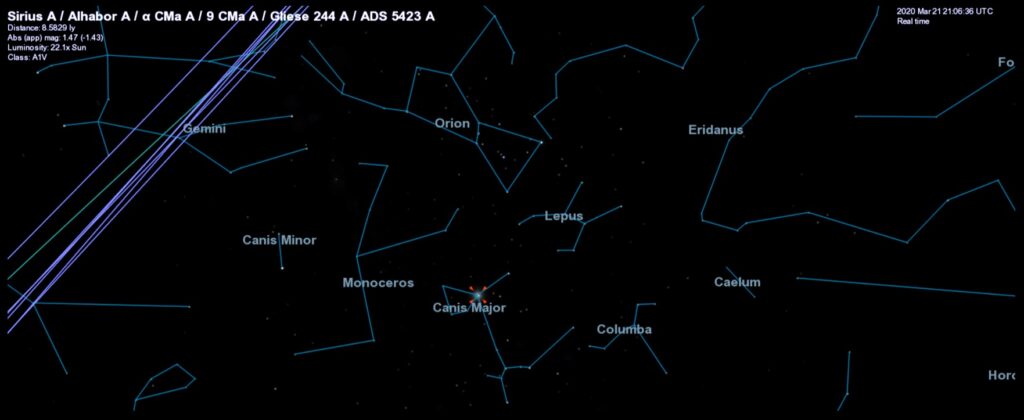Sirius is in the constellation of Canis Major, the Greater Dog, near Orion. This image was made using the Celestia app, and the lines you see at upper left are the orbits of the planets, marking the plane of the solar system and the plane of the Earth’s own orbit.The motion of Sirius B around Sirius A can also be spotted. Observe Sirius with a good telescope over a period of 50 years and you will see Sirius B complete one orbit. The video below shows a little more than two complete orbits of Sirius B about Sirius A, from approximately 2020 to approximately 2154. This video is a simulation made with the app Celestia. It shows what you would see if you had a very good telescope (far better than the Hubble Space Telescope, which took the image of Sirius A & B at the start of this post) aimed at the exact same point in the sky for all that time.
As you can see, the motion is complex! Were you expecting something simpler? If you’ve taken an astronomy class or done some self-teaching, you might have expected something like the video below. It shows what you would see if you had a very good telescope aimed on Sirius A for all that time. It looks like the textbook case of an orbit—Kepler’s laws of orbital motion in action.
What was happening in that first video, with all those crazy motions? Well, it turns out that those crazy motions tell us quite a bit of information about the Sirius system.
First, consider the rapid looping motion of both A and B that you saw in the first video. That is what is called “annual parallax”. It is caused by the motion of the Earth around the sun. As the Earth circles around the sun, that circling motion is reflected in the nearby stars, as seen in the diagram below. This effect is seen only in nearby stars, however; the farther away a star is, the weaker is this effect. This is because the more distant the star, the smaller the size of the Earth’s orbit is relative to that distance.
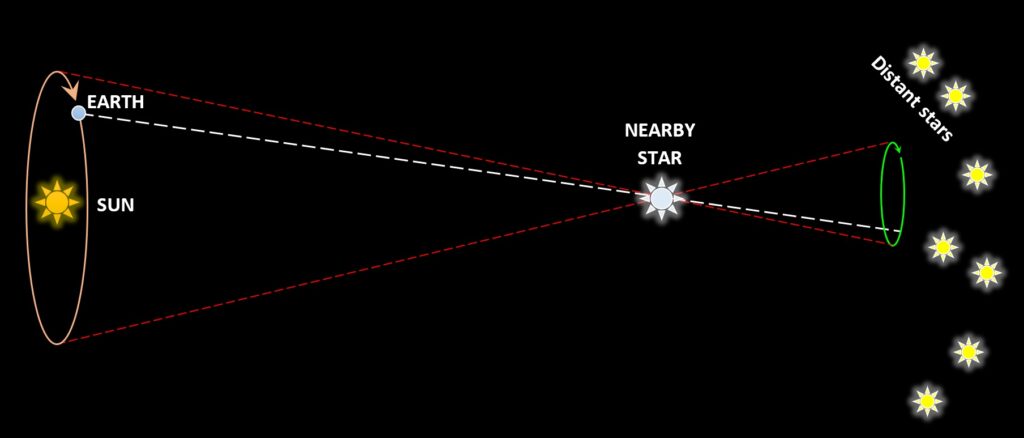Annual parallax. As Earth circles the sun, the line of sight from Earth to a nearby star (white dotted line) changes, causing the star to appear to have a looping motion (green curve) against the background of space and the more distant stars as seen over the course of a year. This effect can only be seen in nearby stars, because the farther away the star is from the sun, the narrower the parallax angle (the angle between the two red dotted lines). For most of astronomy’s history, this parallax effect could not be observed, and the failure to observe it was taken as evidence that the Earth was not in motion. Parallax was finally observed in the 1830s by F. W. Bessel—at a time when telescope technology had advanced sufficiently for telescopes to be able to detect it.If a star is located on the plane of Earth’s orbit, the star’s parallax motion will be back and forth, as seen at left in the figure below. If the star is located straight above the plane of the Earth’s orbit, the star’s parallax motion will be circular, as seen at right. The closer a star is to the plane of the Earth’s orbit, the more back-and-forth and the less circular it will be.
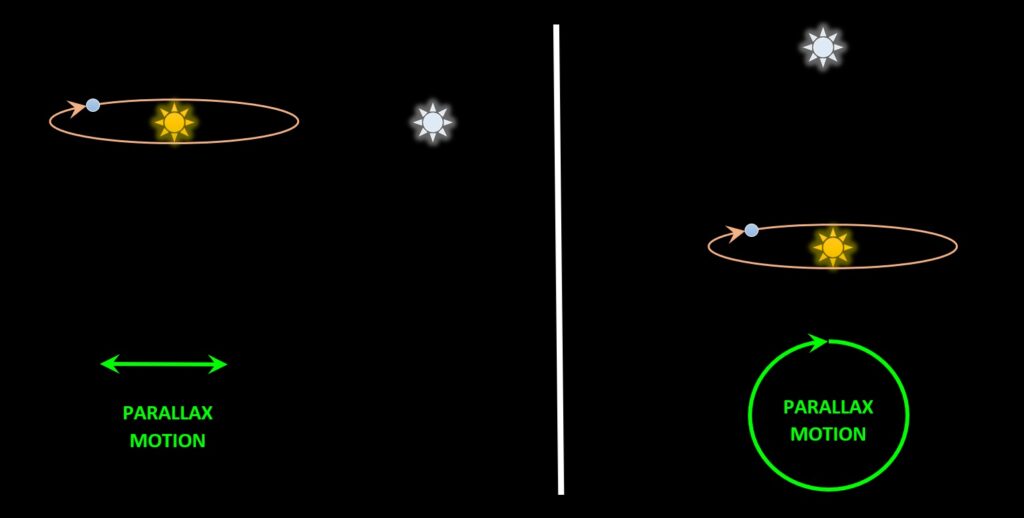Parallax motion (in green) as seen in a star that lies in the plane of Earth’s orbit (left) and above the plane of Earth’s orbit (right).The next video shows this motion for the star Pollux in the constellation Gemini (which is near the plane of Earth’s orbit in the sky) and for the star 36 Dra in the constellation Draco (which is far from the plane). Note how Pollux moves back-and-forth, while 36 Dra moves in a circle. Note also how the parallax motion is weaker in 36 Dra than in Pollux, indicating that 36 Dra is more distant than Pollux.
Next let us look at Sirius A and Pollux, seen side-by-side. Now Pollux (left) has a motion weaker than Sirius A (right, which also drifts across the screen because of Sirius B, as we will discuss in due course). So, Pollux is more distant than Sirius A.
In fact, we can do better than just determine that Sirius is closer than Pollux which is closer than 36 Dra; we can in fact determine the distance of each star. As you can see from the parallax figures above (the ones that show the parallax motion in green), parallax movement is just a matter of angles. In a long, skinny triangle, there is a simple relationship between the length D of the longer leg of the triangle, the length S of the shorter leg, and the triangle’s narrowest angle {a}, as seen in the figure below.
S, D, and the angle {a} are related by the equation D = S/a if {a} is measured in radians.First we measure the size of a star’s parallax motion {a} in units called radians. Just as there are 360 degrees in a circle, there are
2 x Pi = 2 x 3.14159… = 6.28319…
radians in a circle. Then the distance D to that star is calculated via
D = S/a
as in the figure above. But in the case of parallax, S is just the distance from the sun to the Earth. The sun-Earth distance is one Astronomical Unit or one AU. So now we have
D (in AU) = 1/a (in radians)
For Sirius, the parallax is {a} = 1.83846 millionths of a radian, so its distance is
D = 1/1.83846 = 0.5439 million Astronomical Units
or 543,900 AUs. Light takes 8 minutes and 20 seconds (8 & 1/3 minutes) to travel the one AU from the sun to the Earth. Light would then travel from Sirius to Earth in
543,900 x 8 & 1/3 minutes = 4,532,500 minutes.
There are 60 minutes in an hour, 24 hours in a day, and 365.25 days in a year, so
1 year = 60 x 24 x 365.25 = 525,960 minutes.
So, 4,532,500 minutes is
4,532,500 / 525,960 = 8.6 years.
Light therefore takes 8.6 years to travel from Sirius to Earth. Sirius is 8.6 light-years away!
That distance is just the first bit of information we can learn about Sirius from its motions. Parallax is in fact the only direct means we have of measuring the distances to the stars. Using parallax in the same way we did with Sirius, we find that the distance of Pollux is 36 light years, and the distance of 36 Dra is 75 light years.
Once we know how distant Sirius is, we can easily determine how powerful it is by comparing Sirius and the sun and factoring in their distances (see last week’s post for all the details on this). Sirius turns out to have over 20 times the light output power of the sun—that is, over 20 times the luminosity of the sun.
So, we know that Sirius is a star system 8.6 light years away that exceeds the sun’s light output by over 20 times. And we haven’t even messed with the orbit of Sirius B. Next week we will see what else we can learn from the motions of Sirius.
*To any wag who wants to say “Sirius is not the brightest star in the sky, the sun is”, I say “O bother”.
