This is the second in a series of posts about black holes and the black hole discussions that took place at the 25th Seven Pines Symposium in Stillwater, Minnesota, where I was a participant in May. Click here for the first in the series, which is all about Seven Pines and the black hole talks there. Today’s topic is the basic physics behind the idea of black holes.
This might seem hard to believe, but the idea behind black holes has its roots in everyday experiences. What everyday experiences? Doing chin-ups or push-ups, pushing a shopping cart, and separating socks that come out of the dryer.
Four fundamental forces have been identified in nature. Two of these forces, the strong nuclear force and the weak nuclear force, do not extend beyond the nucleus of the atom. Because these forces have such limited range, we do not observe them in the world around us. They are involved in the working of atomic nuclei, and that is all.
The other two fundamental forces of nature, the gravitational force and the electromagnetic force, govern the world we see and observe on a regular basis. Both of these forces are “action-at-a-distance” forces, meaning they act across a distance without some obvious means of transmitting the force. For example, two socks fresh out of the clothes dryer may draw together via “static cling”, even though they are not in contact, and have no physical thread connecting them and pulling them toward one another.
Electromagnetism is a force between particles that depends on something I am going to call (for the moment — bear with me) electrical oomph. We experience electrical forces when we notice the static cling between those socks, or when our hair is standing up due to “static”. The electromagnetic force is fairly strong, so we can notice it even when there is not a large amount of electrical oomph present.
Electromagnetism also is what holds atoms together. It holds an electron in orbit around a proton in a hydrogen atom; it holds sodium and chlorine atoms to each other in salt. Thus electromagnetism is what produces the strength that a salt crystal, or a thread, has. Most contact forces you feel, like the unpleasant force felt when you bump your head on something that has some inherent strength or rigidity, are therefore electromagnetic. In fact, with the exception of your weight, every force you’ve ever experienced has been electromagnetic.
Your weight is gravitational. Gravity is a force between particles that depends on the particles’ gravitational oomph. While gravitational forces act between all objects, the force of gravity is typically very weak. Only the Earth has enough gravitational oomph to produce gravitational forces that we regularly notice. We experience the gravitational force when we notice our own weights, like when doing push-ups or chin-ups. Gravity is also what holds the moon in orbit around the Earth, the Earth in orbit around the sun, and so on for everything else orbiting in space.
There is great similarity between gravity and electromagnetism. The gravitational force between object A and object B increases in proportion to the gravitational oomph of each object, and decreases in proportion to the square of the distance between the two objects. The electromagnetic force between object A and object B increases in proportion to the electrical oomph of each object, and decreases in proportion to the square of the distance between the two objects.
However, electromagnetism can be repulsive as well as attractive. Gravity can only be attractive. Because of this, electromagnetic forces are broadly nullified, so that electromagnetism is not a factor in holding the moon in orbit around the Earth. Gravitational forces, comparably weak though they may be, are never nullified.
Newton’s Second Law of Motion says that when a force acts on an object, the object reacts. The amount of reaction depends on the amount of matter present in the object, or its mass. We measure mass in kilograms (one kilogram is the mass of a liter of water).
If you give a hard push to an empty shopping cart, it reacts dramatically. It goes. It accelerates. You will probably have to go chase after that empty cart you pushed before it hits someone or something.
If you give the exact same hard push to a shopping cart full to the brim with big bags of potatoes bought for the making of mashed potatoes at your church picnic, that cart will react far less dramatically. It won’t go, or accelerate, nearly so much. The empty cart has much less matter in it — much less mass; many fewer kilograms.
Now things get weird.
You see, electrical oomph has nothing to do with mass and kilograms. Electrical oomph is actually called “electric charge”. Socks from the dryer are attracted to each other more if they have more electric charge. They will react to that force of attraction less if they have more mass (if they are thick socks rather than thin socks).
But gravitational oomph actually is mass. Two asteroids are attracted to each other more if they have more mass. They will react to that force of attraction less if they have… more mass. This is why, as Galileo supposedly showed, a cannon ball and a musket ball both fall to the Earth at the same rate. The greater force of gravity on the cannon ball is cancelled by the lesser reaction to that force.
Why would this be? Why would an “action-at-a-distance” force have any connection to quantity of matter? Why doesn’t gravity depend on a “gravitational charge” separate from mass, like electromagnetism does?
Albert Einstein proposed that the explanation for this is that gravity is in fact the exact same thing as acceleration. That’s why the same quantity, mass, is involved in both gravity and Newton’s Second Law. There is no physical difference between a uniform gravitational field, like is found on Earth’s surface, and a constant acceleration.
Here on Earth’s surface, if you hold out an object like a golf ball (or a cannon ball, or a musket ball) and release it, it will accelerate downward at a constant rate, increasing in speed by 22 mph each second that it falls. In metric units, 22 mph is 9.8 meters per second. So the ball accelerates at 9.8 meters per second per second, or 9.8 m/s2.
Consider a classroom, on Earth, in which a professor is giving a lecture on gravity and falling objects. A golf ball dropped in the classroom accelerates downward at a rate of 9.8 m/s2 (below, left). However, suppose the classroom were in space (no gravity), in a rocket ship that was accelerating at a constant 9.8 m/s2. The class could not tell the difference between that and Earth’s uniform gravitational field (below, right). While the professor was holding the ball, it would accelerate with the ship. When the professor released the ball, it would stop accelerating and would move with constant velocity (Newton’s First Law — “an object in motion remains in motion, etc.”). It would coast.
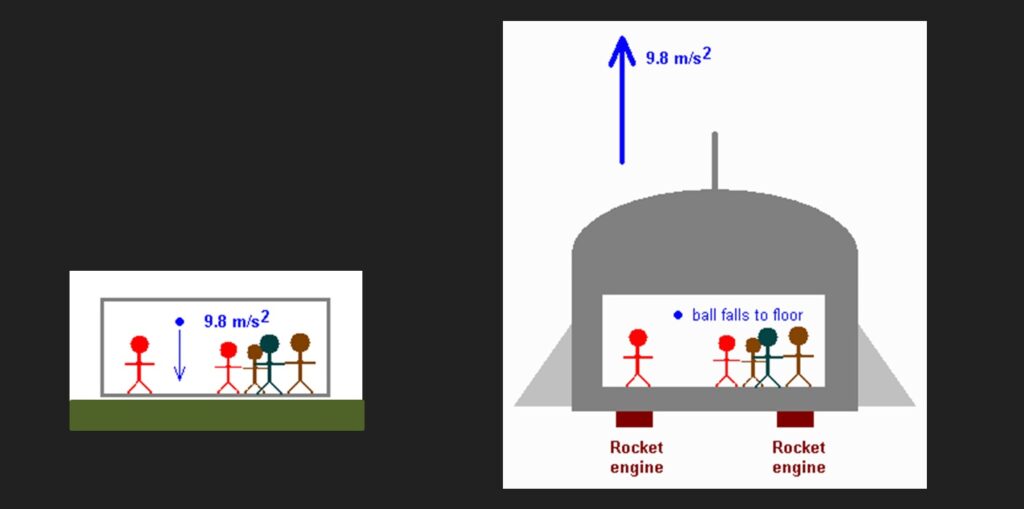
However, the ship would continue to accelerate, and so the distance between the ball and the floor would decrease. The ball would “fall” to the floor. Or, put another way, the ball would coast in space, and the floor would catch up to meet it. There is no difference between “the fall” and “the coast”.
This is just like in a car. When you step on the gas and accelerate forward, loose objects on the dashboard “fall” backward as though there were forces acting on them. When you step on the brake, loose objects “fall” forward. To make things perfectly clear here, whatever direction our rocket ship is pointing, the ball always “falls” in the opposite direction at a rate of 9.8 m/s2. There is no “up” or “down” in space when there is no gravity.
An interesting consequence springs from Einstein’s idea that acceleration and gravity are equivalent! Suppose the “classroom in the rocket ship” has a lamp on the wall that emits a light pulse at right angles to the motion of the ship, as shown below. As the rocket accelerates forward, the light pulse is left behind. The result is that the pulse “falls to the floor” as seen by the occupants of the ship, who cannot tell if they are accelerating or if they are in a gravitational field. Note that the pulse moves horizontally with constant speed as seen from outside the ship.*
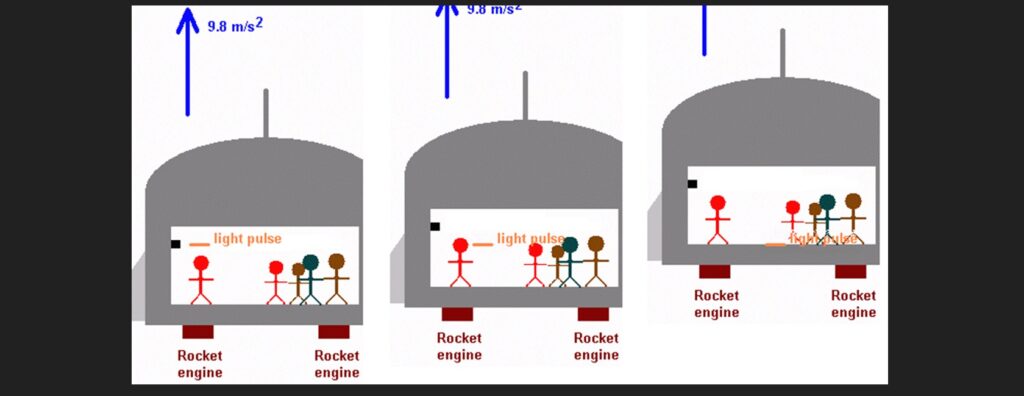
Of course the diagram above is wildly exaggerated. Light moves so rapidly that it would “fall” very, very little as it crossed a room in which the acceleration was only 9.8 m/s2. But nonetheless, it would “fall”. And were the acceleration of the ship great enough, the “fall” could be significant.
If gravity is in fact the exact same thing as acceleration, then a light pulse emitted from a lamp on the wall of a classroom in a uniform gravitational field must also fall towards the ground. In fact, it does, but the effect is quite small. However, the effect of light being deflected or bent by a gravitational field is well-documented.
The most dramatic examples of gravity bending light are the examples of “gravitational lensing” found in astronomy. If a massive object such as a galaxy lies between an observer and a distant object, the galaxy’s gravitational field can bend light from the distant object toward the observer as shown here.

To the observer, light from the distant object seems to be coming from above and below the galaxy. The result is that the observer sees an image of the distant object appearing above and below the galaxy. Of course this happens in three dimensions, so images of the distant object can appear to the left and right of the galaxy as well. This is what is known as an “Einstein Cross”.
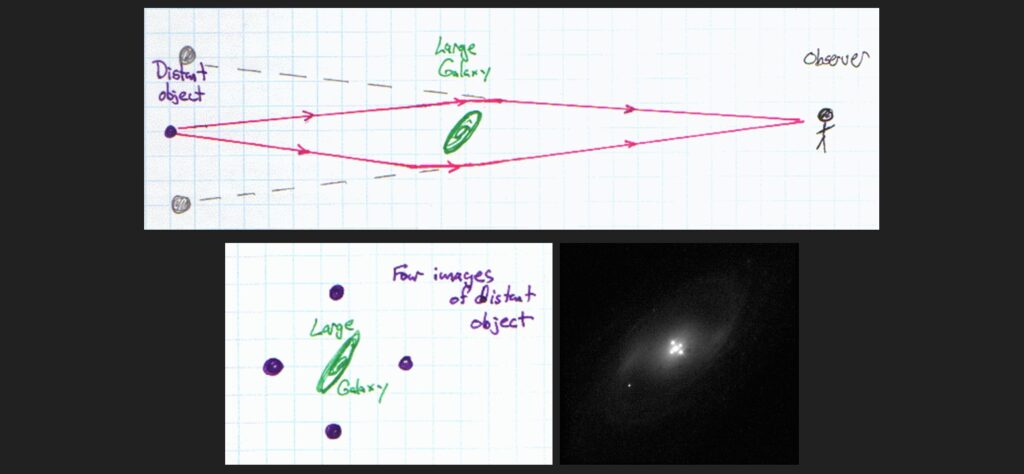
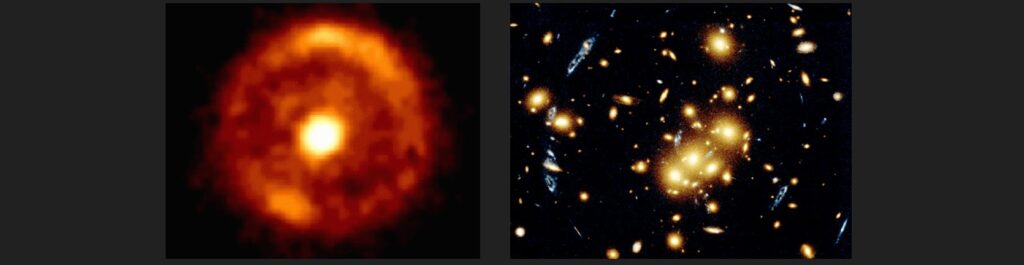
If the alignment is just right, it is possible for light from the distant object to converge from all directions around the galaxy toward the observer. The result of this sort of unique geometry is an “Einstein Ring” as pictured below left. However, gravitational lensing usually doesn’t produce such neat, clean shapes. The usual result of gravitational lensing is multiple images, often distorted into arc shapes (partial rings), as seen in the image below right. Here all the blue-colored images are all the same object! The cluster of galaxies at the center of the picture has lensed the light from that distant object.
Gravity can’t exert a “force” on light; Newton’s Second Law says a force is that which causes a mass to accelerate, and since light has no mass, a “force” on it is meaningless. We must think of gravity in another way than as a force. Light follows a straight-line path when not in a gravitational field, so we think of gravity as a “warping” of space. Light wants to travel in a straight line, but space itself is curved by the presence of a massive object, so the light travels in a curved path, and thus is deflected.
Suppose now that the classroom light pulse is sent out along the direction of the motion of the ship, as shown below. Here we make the ship longer, and put the professor at one end and the students at the other. Again, as the rocket accelerates forward, the light pulse is left behind, at least in a sense (it moves faster than the ship, of course*). That is, during the time between when the students send the light pulse and when the pulse reaches the professor, the speed of the ship will have increased, thanks to the acceleration caused by the ship’s engines. It will thus (according to an outside observer*) take the pulse longer to pass by the professor than it did to leave the students.

Put another way, the time required for the professor to receive the pulse will be greater than the time required for the students to send it. The professor will see the students’ activities as taking more time than the students themselves saw those activities as taking. Thus time is affected by acceleration. If gravity is in fact the exact same thing as acceleration, then this “stretching of time” effect, or “time dilation”, must occur in gravity, too. Thus gravity “warps” time as well as space.
If gravity deflects light, warps space, and warps time, then it follows that sufficient gravity could radically deflect light, and radically warp space and time. We can imagine that there could be an object with such strong gravity that any light that might try to leave it would be bent right back to it; any light waves rising up from it would be stretched out into nothingness. Any light coming in would never get back out. This object would reflect nothing. It would be truly a Black Hole.
Pretty remarkable, huh? Put together chin-ups, shopping carts, and socks fresh out of the dryer, and what do you get? Black holes!
Now we understand the basics of black holes. Next time (two weeks from now): can black holes remember things, or show us the past? Yes, this was discussed at Seven Pines!
Click here for all the “Black Holes at Seven Pines” posts.
*In Einstein’s theory, not only are acceleration and gravity the same thing, but light always moves at a constant speed as seen by all observers, regardless of their own relative motions, and nothing can move faster than light. This complicates the picture of a light pulse seen within the rocket ship classroom, but does not change the basic picture presented here.

