It seems that black holes might be able to “remember” things… but is the range of those memories limited? This is the fourth in a series of posts about black holes and the black hole discussion that took place at the 25th Seven Pines Symposium in Stillwater, Minnesota, in May. Click here for the whole series.
I was a speaker at Seven Pines. I talked about Johannes Kepler. It may seem odd, but my suspicions regarding the limits of black hole memory tie in with the topic of my talk.
In the last “Black Holes at Seven Pines” post, I discussed Peter Galison and Shep Doeleman each bringing up the idea of black hole memory — Galison describing black holes as “the ultimate storehouse of memory” that might even remember him and his family; Doeleman mentioning the idea that black holes could allow us to see Earth in the past, at the time of the dinosaurs, for example. These ideas mean black holes would be a kind of imaging system, a kind of camera: Galison has spoken of black holes as storing frames of a movie of the universe; seeing dinosaurs on Earth implies images.
Imagining systems have limits, however. Your naked eye cannot see fine detail on the moon. Your telescope can see better detail, but if you have ever tried to run the magnification on your telescope up extremely high, you know that there is a limit to what even it can see. It is just like magnifying the image at the top of this post. If you keep enlarging it, you do not see more detail; you just see enlarged pixels. All imagining systems have an inherent limit to their ability to see detail, a natural “pixel size” that is determined by the wavelength of light they are receiving and by their “aperture” (aperture being the size of the main lens or mirror of the system; if you have a pair of 50 mm binoculars, the aperture is 50 mm).
Kepler, like other astronomers of his time, and like astronomers before and even somewhat after him, did not know this. He was unaware that when he looked at a star, what he saw did not reflect the actual size of the star (because the star fell below the natural pixel size of the eye, or even of any telescope of the day) — whereas when he looked at a tree down the way, or at the moon, what he saw did reflect the actual size of the tree or moon (because those objects appeared larger than the natural pixel size of the eye). The image below shows an illustration by the nineteenth-century astronomer John Herschel of a star seen through a very small aperture (~1 cm) telescope, such as was used in Kepler’s time. What looks like the globe of the star is actually just the natural “pixel” (or “Airy disk”, named for the nineteenth-century astronomer G. B. Airy) of the telescope. The apparent size Herschel shows here is a product of optics; in terms of straight geometrical dimensions, the star should be vanishingly small.

Kepler was a Copernican. He understood that in a Copernican universe the stars had to be very far away for them not to reflect Earth’s orbital motion. Therefore, in calculating how big the stars must be to appear as large as they do despite that distance, he wildly overestimated their sizes. And because he wildly overestimated their sizes, he wildly underestimated their surface brightnesses.
Thus Kepler concluded, based on solid, reproducible measurements and simple calculations, that stars were far larger than, yet far dimmer than, the sun. That meant that the sun had to be the universe’s unique, tiny brilliant central body. And every real astronomer, who actually knew what the sky looked like, had to agree with Kepler. People like Giordano Bruno, who declared that the stars must be other suns, did not know their stuff, and Kepler said so. This would be the situation until people began to figure out that there was something funny about stars (they began to figure that out when they carefully observed the moon passing in front of stars, and noticed that the stars’ light did not diminish gradually, but almost instantaneously). Kepler’s story matters because it shows that science initially revealed a Copernican universe far different from the one we now know, and because it cautions us to make sure we really understand instruments such as telescopes.
If a black hole is going to “image” the Earth, it is going to function as a telescope or camera of sorts. It should be bound by the same laws of physics as other telescopes. That means it will have its own natural “pixel size”. What will be the pixel size of a black hole?
It turns out that the pixel size of a black hole that has an apparent diameter seen from Earth of 100 microarcseconds or 100 μas (millionths of an arc second, where an arc second is 1/3600 of a degree, and a degree is the width of two full moons, side-by-side) will have a natural pixel size of 1384 meters at Earth. That’s more than a kilometer, and almost a mile. The formula+ is
Pixel size at Earth in meters = 138,400 / black hole apparent diameter in μas
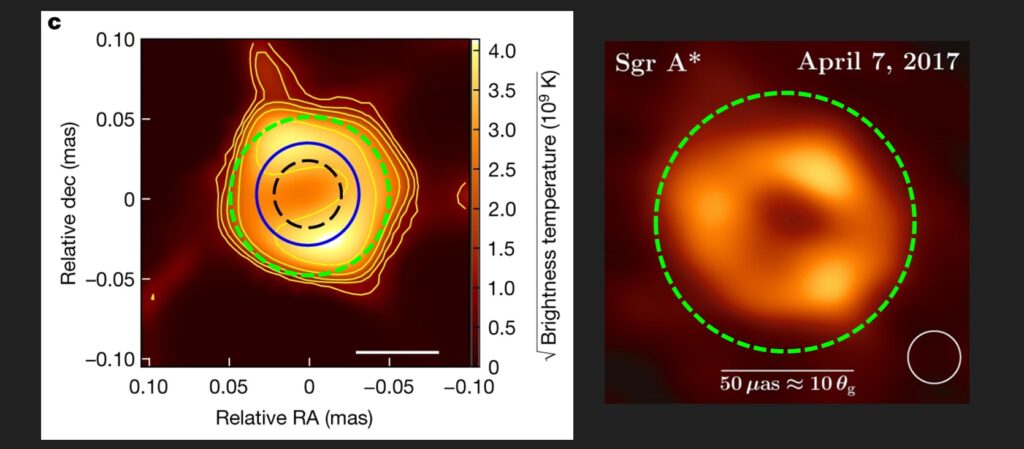
Both the M87* and Sgr A* (Milky Way) black holes have diameters of under 100 μas. In the figures below, taken from Nature and The Astrophysical Journal Letters, the green dashed circle has a diameter of 100 μas. So the “pixel size” of any “memory image” these black holes might form of Earth will be larger than 1384 meters — indeed, it might be about a mile in diameter. The smallest detail on Earth that these two black holes could “see” and “remember” would be roughly a mile across. Black holes might remember wildfire smoke stretching across a continent in the light whipping around them, but they could record no images of dinosaurs or human families.
What would it take to record dinosours or people? Well, to have a pixel size of 1.384 meters, namely 1000 times smaller, would require a black hole with an apparent size 1000 times larger, or 100,000 μas. But that will not record dinosaurs or people very well.
A pixel size of 1.384 mm, 1000 times smaller still, would do. That would not be the most “high definition” record of people, but it would be OK — sort of like old-school analog TV. That would mean a black hole with apparent size of 100,000,000 μas. That is 100 arcseconds, or roughly twice the apparent diameter of Jupiter at its closest approach to Earth!
Thus, for these black holes to record images of the dinosaurs or people on the Earth would require them to be a million times closer than they are. So M87* would have to be 54 light years distant, rather than 54 million light years. Sgr A* would have to be 0.027 light years away, instead of 27,000 — closer than the Oort Cloud! I’m no black hole expert, but I’m guessing that having those big black holes that close would be kind of bad.
Given all this, I do not think that black holes can be the “ultimate storehouse of memory”. I’m counting on God to play that role, to keep those vivid, video-like memories of my sons’ birthdays as kids (see the last “Black Holes at Seven Pines” post). If God knows when a sparrow falls to the ground and knows the hairs on my head, God will know those birthdays, will know every detail of Galison’s life and family, and will have record of the dinosaurs. Black hole memory is a cool idea, but I think the laws of optics shoot it down.
This problem with black hole memory, and the connection to Kepler, came to me while González de Arrieta, Knox, Doeleman and I were walking and talking after lunch one day. I tossed out the basic outline of what is in this post, throwing a smelly wet horse blanket on the whole memory idea. Doeleman thought about this briefly, and then proffered an idea that reflects a really optimistic, can-do attitude: we might still be able to do black hole dino-spectroscopy! I love it.
Next “Black Holes at Seven Pines” post: Scientists and philosophers debate whether we are really detecting black holes! Stay tuned.
Click here for all the “Black Holes at Seven Pines” posts.
+Here’s the math for the formula:
The resolving power or natural “pixel size” θ of an optical system with aperture A (in this case the black hole) can be estimated by the Airy disk/Rayleigh criterion:
θ = 1.22 (λ/A)
Here λ is the wavelength of light passing through the aperture. But θ is an angular measure. To determine what size S in meters this would translate into on Earth, at a distance D from the aperture, we use θ = S/D.
S/D = 1.22 (λ/A)
S = 1.22 (λD/A)
Meanwhile, the black hole seen from Earth has angular size α. This is related to its diameter (the aperture A) via α = A/D. So αD = A. The equation for S can now be written
S = 1.22 (λD/αD) = 1.22 (λ/α)
Choosing λ = 550 nm, the middle of the visible spectrum, we get
S = 1.22 {(550×10-9 meters)/α} = (671×10-9 meters)/α
But here α is in radians. 1 rad = 360/2π degrees = 57.296 deg. 1 degree = 3600 arcseconds. 1 arcsecond = 1,000,000 μas. Thus 1 rad = (360/2π)×3600×1,000,000 = 2.063×1011 μas. 1 μas = 1/2.063×1011 rad = 4.848×10-12 rad. So the formula is as follows for α in μas:
S = (671×10-9 meters)/(α×4.848×10-12)
Since (671×10-9)/(4.848×10-12) = 138,400, then
S = 138,400/α
where S is in meters and α is in μas.

