This is the fifth (and last) in a series of posts about black holes and the black hole discussions that took place at the 25th Seven Pines Symposium in Stillwater, Minnesota, in May. I was a speaker at Seven Pines — not on black holes, but that did not stop me from opening my mouth on the topic, as you will see! Click here for the whole series.
As discussed in the last two posts in this series, one of the black holes topics that really struck me at Seven Pines was black holes and “memory”. Another, however, was detecting gravitational waves from black holes — and whether we have directly detected them at all.
To understand gravitational waves, let’s think about gravity for a minute. The gravitational pull between two mass-having objects decreases as the square of the distance between them. If you decrease the distance between two objects by half, the gravitational pull between them increases by a factor of four; if you double the distance between them, the gravitational pull decreases by a factor of four.
Imagine you have two objects of equal mass (‘M’) connected by a rod of length ‘D’, as shown in the diagram below. These two masses are set apart from a smaller mass (‘m’), so that the center of the rod is also a distance ‘D’ from ‘m’. The two ‘M’s will exert gravitational pulls on ‘m’. To keep things simple, we will say that a single ‘M’ located 1 distance unit from ‘m’ will create a 1 force unit gravitational pull on ‘m’.
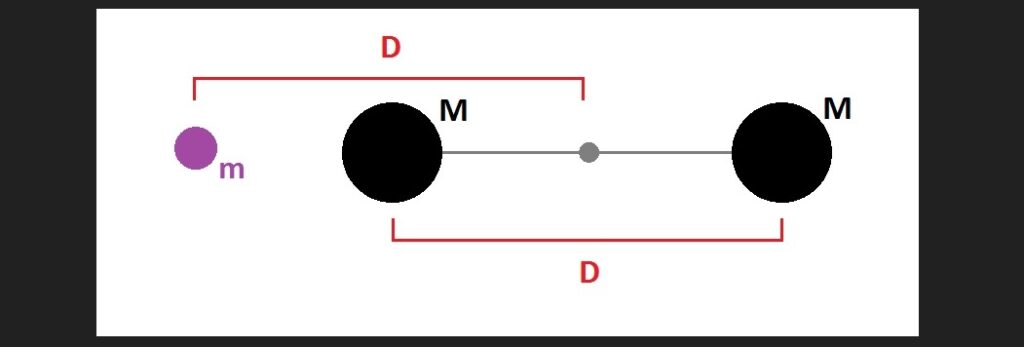
Now, suppose that ‘D’ is 2 distance units. The distance between the left-hand ‘M’ and the smaller mass ‘m’ is therefore 1. The gravitational pull of ‘M’ on ‘m’ is thus 1 force unit.
The distance between the right-hand ‘M’ and ‘m’ is 3. The pull it exerts on ‘m’ is less than the pull of the left-hand ‘M’ by a factor of 3 squared, or 9. So the pull of the right-hand ‘M’ on ‘m’ is 1/9, or 0.111. The total pull on ‘m’ is therefore 1.111 force units.
Now rotate the two ‘M’s around the center of the rod, by a quarter turn, like below. The net pull on ‘m’ will be much less.
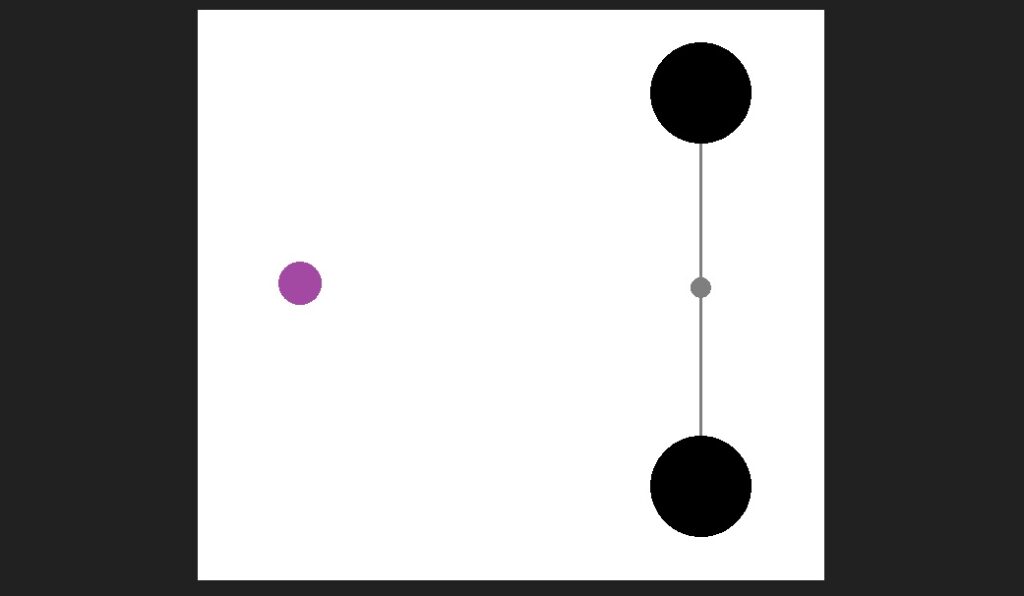
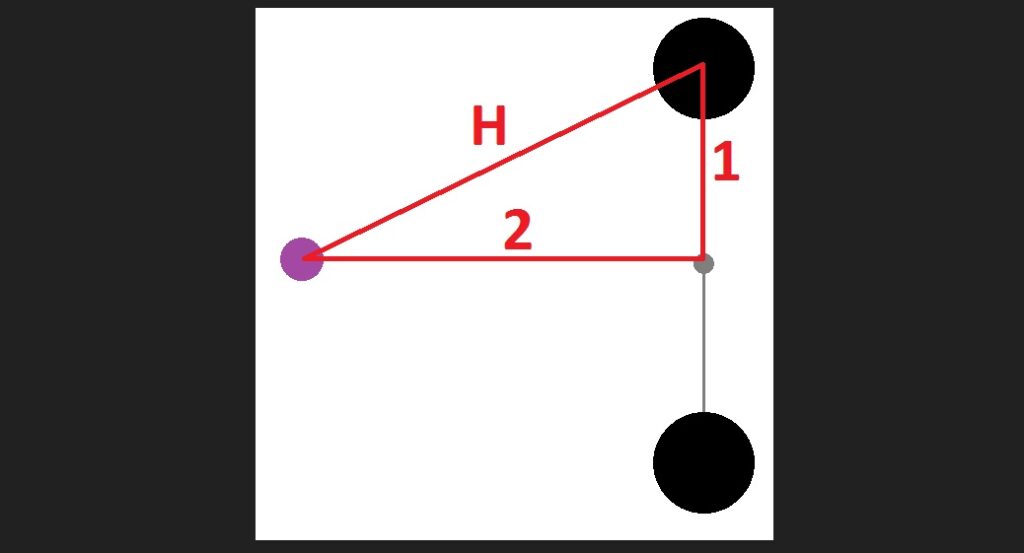
The distance between each ‘M’ and ‘m’ will now be the hypotenuse ‘H’ of a right triangle whose sides are length 1 and 2, as shown below. I will skip the Pythagorean Theorem here — it is obvious that ‘H’ is greater than 2, which means each ‘M’ will pull on ‘m’ with a force that is weaker by a factor of more than 2 squared (that is, 4) less than the pull the left-hand ‘M’ had previously exerted. The total pull of both ‘M’s in this configuration will be well less than half of what it was previously.
Now imagine that we set the two ‘M’s into steady rotation about the center of the connecting rod, and that we hang ‘m’ from a cord so that it becomes the bob of a pendulum. What is going to happen? The pull on the pendulum will vary as the two ‘M’s spin; that will set the pendulum swinging. The motion of the two ‘M’s will drive the pendulum via gravitational force.
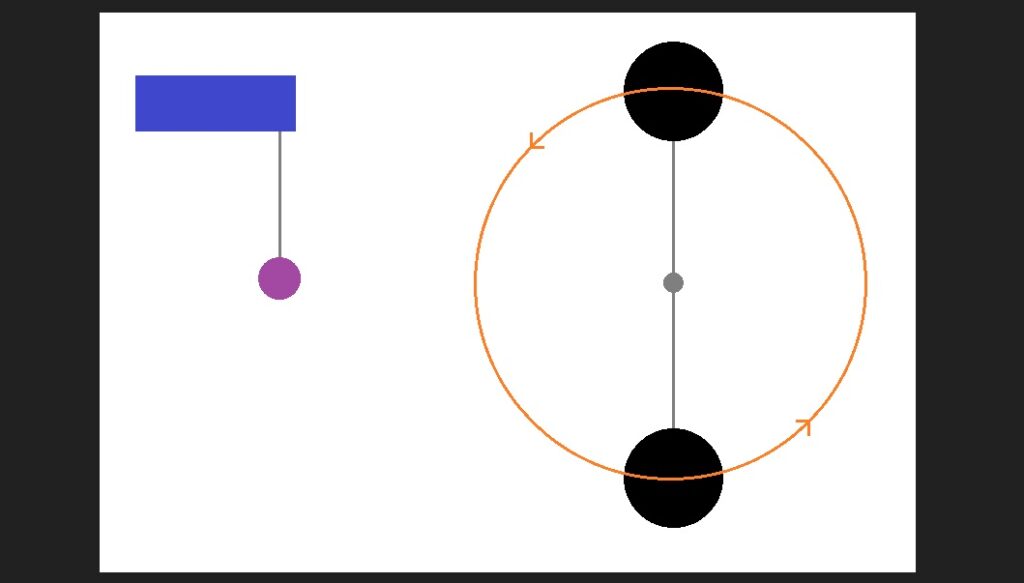
If we increase the distance between ‘m’ and the center of the rod, we would expect this driving effect to decrease, but not to disappear.

This illustration is very limited, and is based on the idea of gravity as a force, as Isaac Newton theorized it to behave. As we discussed in the second post in this series, according to Einstein, gravity is not just a “force” — it is a warping, or a distorting, of space and time. If the two ‘M’s are steadily rotating, the space-time distortions must change in a regular fashion, becoming gravitational waves that travel outward and have an affect on ‘m’, jostling it back and forth. It is as though the two ‘M’s were two connected boats on a pond, such that their circling creates waves that propagate outward and jostle a third, smaller boat, namely ‘m’.
Now let us imagine that the two ‘M’s are connected, not by a rod, but by a strong spring that draws them together. They are set spinning on the pond. Their motion causes the spring to be stretched quite a bit. Their motion disturbs the water, however, generating waves that carry away the energy of that motion. They do not just slow down, because the spring pulls them together, like a spinning ice skater drawing in her arms. So they keep going, and draw together, while their speed — and therefore the waves they generate — is governed by the rate they are losing energy to the waves and the rate of release of the energy stored in the stretched spring.
And this last case is analogous to the case of two orbiting black holes. The black holes (the two large masses or “boats”, ‘M’) are swinging round each other (the spin). They are attracted to each other by their gravity (the spring, which in this case actually pulls harder the closer they get to each other). They are generating waves (gravitational, not water) that carry away their orbital energy. They draw together and merge, and this process generates a specific wave signature which is detected by a gravitational wave detector (the smaller “boat”, ‘m’).
An example of a real such detector is LIGO (the Laser Interferometer Gravitational-Wave Observatory), which is basically a mass that can be jostled by gravitational waves, plus a lot of fancy detectors to detect the slightest bit of such jostling. Daniel Holz of the University of Chicago, who works on LIGO, talked about it at Seven Pines on May 13 (subbing in for Gabriela González of Louisiana State University who at the last minute was prevented by circumstances from talking on it). The famous signature “chirp” from LIGO, produced by gravitational waves given off by merging black holes, was of course part of his talk.
Jamee Elder of Harvard followed Holz, and her talk was titled “The ‘Direct Detection’ of Gravitational Waves”. Her abstract said that she would, “clarify and adjudicate a controversy that arose within the astrophysics community concerning whether or not the first LIGO detection, ‘GW150914’, was the first ‘direct detection’ of gravitational waves”. Does LIGO directly detect gravitational waves? Or, put another way, what does it mean for LIGO to “directly” detect gravitational waves?
Gravitational waves were “indirectly detected” decades ago, by Russell Hulse and Joseph Taylor. Using the Arecibo radio telescope, they observed radio signals from a pulsar in a binary system with a neutron star that showed the system to be losing energy in a manner consistent with it generating gravitational waves. This would be as though the ‘M’ boats in our illustration above had horns on them, and an observer, listening to the horns, was able to deduce from the changing tones of the horns that the boats were circling and drawing toward one another in a manner consistent with their generating waves — but the observer never saw the waves themselves. Hulse and Taylor won a Nobel Prize in 1993 for this work.
Elder noted that Taylor argued that LIGO did not really represent a direct detection of gravitational waves. Taylor had said that,
In the binary pulsar experiment, and also in a LIGO-like experiment, one infers the presence of gravitational radiation based on effects it induces in a “detector.” If a ruler could be used to measure the displacement of LIGO’s test masses, I would grant that detection to be rather more “direct” than one based on timing measurements of an orbiting pulsar halfway across our Galaxy. However, LIGO can’t use a ruler; instead they use servomechanisms, very sensitive electronics… and finally long sequences of calculations to infer that a gravitational wave has passed by. Such a detection, like the binary pulsar timing experiment, is arguably many stages removed from being what most people would call “direct.”
Sticking to our illustration, this would be as though the motion of ‘m’ as it was jostled by the waves was so small that it could not be seen, and had to be deduced from signals generated in fancy detector circuitry. What’s the difference, Taylor seems to be saying, between deducing the existence of waves from one set of signals and from another, when in either case you cannot see the waves?
Talks at Seven Pines are done in pairs, with a lengthy Q&A/discussion session afterwards in which both speakers, in this case Elder and Holz, are on the floor together.* The Holz-Elder discussion really got going. At one point Shep Doeleman asked for a show of hands for who thought that the Event Horizon Telescope had actually imaged a black hole. Not all hands went up! It was lively.
Holz seemed bemused by it all — cheerfully and pleasantly bemused, mind you, but bemused nonetheless. Hey, who wants to work like a dog on LIGO only to hear smart people talking about whether it is any more of a detection of gravitational waves than work done decades ago?
Or, worse yet, to hear that your opinions as a LIGO scientist might not count? Early in his talk Holz commented on a line from a draft paper Elder had given to the Seven Pines participants (all speakers at Seven Pines are asked to provide participants with reading material to look over prior to the talks): “philosophy of science frequently involves conceptual clarification, revision or even outright disagreement with what scientists take themselves to be doing”. Later on Holz would jokingly ask if he had missed any discussion among the Seven Pines participants in which we had decided that we could definitively prove that LIGO had not detected anything and that in fact black holes don’t even exist!
Well, somewhere in all the lively talk I decided to wade into the debate on the side of LIGO. Do I know anything about this stuff? No. But what the heck — it was the last formal pair of talks of the conference.
I put my hand up. LIGO does detect gravitational waves directly, I said. In theory, it could detect waves we generated ourselves, if we, for example, constructed a pair of massive, connected metal spheres some distance from LIGO and set them spinning rapidly about each other (like in the illustrations above!). LIGO could detect those waves. We could vary the spin rate and see that reflected in the LIGO data. That seems direct to me, regardless of how much fancy circuitry is involved.
That was my contribution. I feel that the fact that LIGO could (in theory) detect gravitational waves that we ourselves generate and control makes LIGO demonstrably (in theory) “direct” in detecting those waves in a way that deducing their existence from pulsar radio signals is not. Some other mechanism — angels, anyone? — could cause energy loss in orbiting pulsars in such a way as to exactly mimic what we expect from gravitational waves, and fool the Hulse-Taylor method. Those tricky angels could not fool LIGO! (No, I did not mention angels in my comments.)
Well, despite me knowing nothing, Holz jumped right on my idea, pointing to the existence of LIGO’s “Newtonian Calibrator” (a version of the spinning spheres — click here to read all about it), which I did not know existed. There we go. Hey, I did not grossly embarrass myself with my comments after all! For the rest of the discussion I was on Team “LIGO directly detects gravitational waves”. I still am.
This concludes my series of posts on black holes at Seven Pines. With luck, you now know a bit more about the basics of black holes and gravitational waves. And, with luck, I have been able to give you a little window into what those who are true experts on these things have to say about them — when they are all having a good time eating, drinking, and discussing at the Seven Pines Symposium in Stillwater, Minnesota.
*The exception to the “pair” rule was me. The person I was paired with, Anna Marie Roos of the University of Lincoln (UK) was unable to attend at the last minute. She was able to send in a recorded presentation. That left me to handle the hour-plus Q&A/discussion solo, after doing my own talk. It was at first quite invigorating. But as the discussion drew to its finish I was getting pretty worn out and losing my train of thought. At the very end Jim Peebles was asking me something, and we were both talking past each other, and now I cannot even recollect what his question was. My students at my old college, Jefferson Community & Technical College in Louisville, Kentucky, can take heart in knowing that I was no less attentive to their questions than I was to those of a Nobel laureate.

