With the eclipse coming on Monday, and with Vatican Observatory Director and boss blogger for The Catholic Astronomer Br. Guy being in Hopkinsville, Kentucky for the eclipse, you can bet you will see a lot of eclipse posts from The Catholic Astronomer’s Kentucky blogger! (Click here for Monday’s post.)
With the eclipse coming on Monday, and with Vatican Observatory Director and boss blogger for The Catholic Astronomer Br. Guy being in Hopkinsville, Kentucky for the eclipse, you can bet you will see a lot of eclipse posts from The Catholic Astronomer’s Kentucky blogger! (Click here for Monday’s post.)
Here’s something you probably don’t think of when you think of eclipses: measuring the distance to the moon. But you can use an eclipse to measure the distance to the moon. You just need observers in two different places.
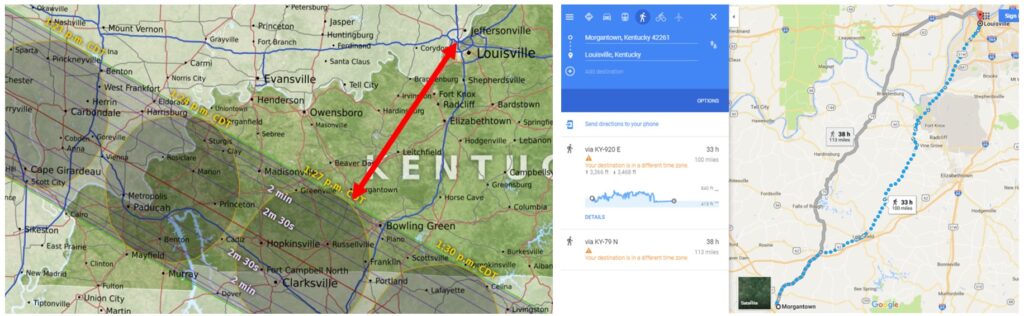
Imagine one observer located in Louisville, where the maximum coverage during the eclipse will look like the image at below left, and a second observer located on the edge of the zone of totality, where the moon just covers the sun. One such place in Kentucky is Morgantown. Why is the position of the moon against the sun shifted slightly between the two locations? Because of the difference in viewing position between Louisville and Morgantown.
How much of a shift is it? Well, the sun measures 0.5 degrees in diameter. There are 90 degrees between the horizon and the point directly overhead, that is, between the horizon and the zenith: 180 suns would line up edge-to-edge between the horizon and the zenith. We can compare the whole sun against the fraction of the sun’s diameter visible from Louisville, and the fraction of the sun’s diameter visible from Morgantown (that is, zero). We see the moon’s position is shifted by about 1/20 the sun’s diameter.
That is 1/20 of 0.5 degrees, or
(1/20) x 0.5 = 0.025 degrees
Now 180 degrees equals π radians, or, 180 degrees equals approximately 3.14159 radians, so this is
0.025 x (3.14159/180) = 0.00043633 radians
So the distance between Louisville and Morgantown causes a 0.00043633 radian change in the moon’s position. So what is the distance between Louisville and Morgantown? Suppose you just hop in the pickup truck and drive it off, taking all the shortcuts to be as straight as possible. The distance comes to about 100 miles.
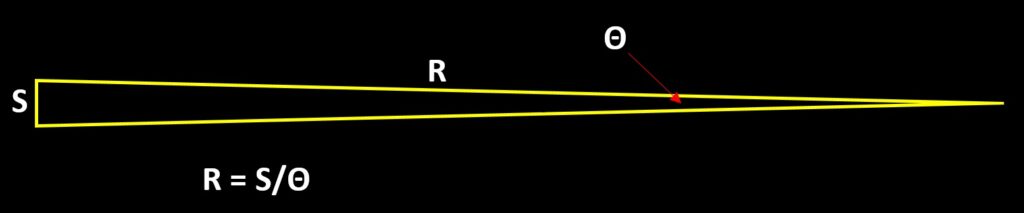
Now for a little geometry. In a long skinny triangle, distance and angle (in radians) are related by the formula below.
So, S is our 100 miles. The angle Θ is 0.00043633 radians. Thus the distance to the moon, which is the long part of the triangle, R, is
R = S/Θ = 100/0.00043633 = 229,183.31 miles.
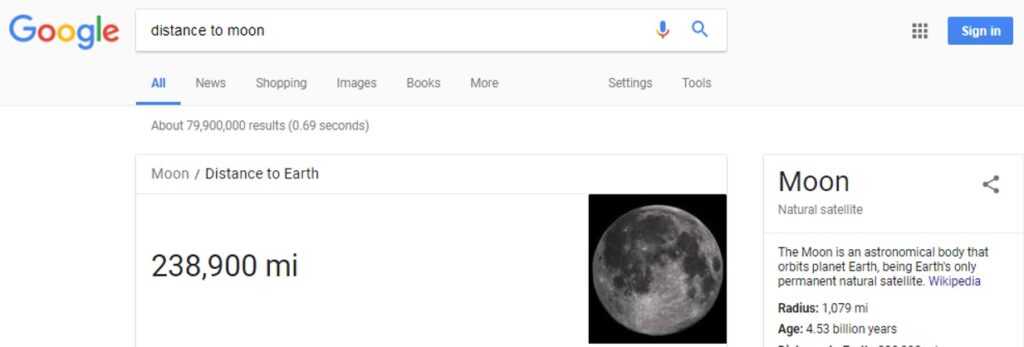
If we Google the distance to the moon we get 238,900 miles. Rounding our value give us 229,200 miles, which differs from Google’s value by only 9,700 miles—a four percent difference! Not too shabby.
Let’s hope the weather forecast for Hopkinsville is not as accurate as this! We want clear skies! The forecast is not looking any better than it did on Monday. In fact, it looks worse! Stay tuned for more eclipse news from Kentucky!