The Title Page of DisquisitionsIn 1614, well before Isaac Newton was even born, a German Jesuit astronomer named Christoph Scheiner and his student, Johann Georg Locher, developed an explanation for how the Earth could orbit the sun. Earth, they said, was like a massive ball, perpetually falling toward the sun. They discussed this in their 1614 book Disquisitiones Mathematicae de Controversiis et Novitatibus Astronomicis, or Mathematical Disquisitions Concerning Astronomical Controversies and Novelties (recently translated by yours truly, and published by the University of Notre Dame Press—click here). This was Locher’s thesis for his degree from the University of Ingolstadt, where Fr. Scheiner taught.
Fr. Scheiner is a relatively well-known figure in the history of astronomy. He is the astronomer with whom Galileo debated regarding sunspots; he would go on to write a monumental 1630 book based on his long-term, detailed solar observations: Rosa Ursina Sive Sol. This book would define solar astronomy for decades. By contrast, not much is known about Locher. Galileo himself devoted quite a few pages of his 1632 Dialogue Concerning the Two Chief World Systems—Ptolemaic and Copernican to making sport of Disquisitions, which was considered Scheiner’s work as much as Locher’s. It was the “booklet of theses, which is full of novelties” that Galileo had his less-than-brilliant character Simplicio drag out in order to defend one or another wrong-headed idea.
But Disquisitions is nothing like Galileo’s negative portrayal of it (by this point, readers of The Catholic Astronomer probably will not be surprised at this, granted the recent discoveries regarding Galileo’s letter to Castelli of 1613, which were the subject of one recent post here, and granted some of the other strange things Galileo says in the Dialogue, which were the subject of a series of posts). There is in fact a lot of cool stuff in Disquisitions. However, its discussion on the physics of an orbit is extra cool.
This discussion treats an orbit as a perpetual fall. It appears in a part of the book that treats the issue of movement downward on Earth. “Everyone,” Locher writes, “even Copernicans, acknowledges heavy bodies to be pulled down toward the center of Earth along a vertical line”. He notes that the downward urge of heavy material is the reason why the terrestrial globe exists, and why its center of gravity coincides with its geometric center. However, because of evaporations and eruptions and other processes on Earth, the center of gravity is changing, and therefore “the globe itself must vacillate with a certain perpetual, but entirely insensible, trembling”. Locher then says that, “perpetual motion is not incompatible with nature.” And, from this statement, he launches into his discussion of orbital “perpetual motion.”
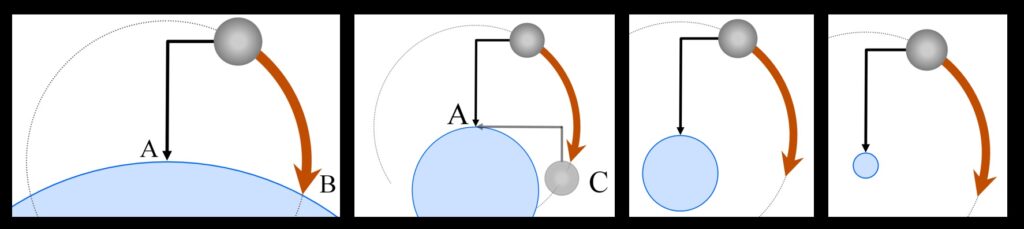
Imagine, says Locher, an L-shaped rod, buried in the Earth. The asymmetry of the rod means that it would topple were it cut off at Earth’s surface. This would be all the more true, he says, were a heavy iron ball attached to the end of the rod, as shown in the figures below. Now, he says, imagine the rod being hinged at the Earth’s surface (at point A in the figures). The heaviness or gravity of the ball (“gravity” here meaning the ball’s action of trying to reach its natural place at the center of the universe—Aristotelian physics was the rule in 1614, with Newtonian ideas about gravity lying decades in the future) presses down on the rod, but the rod keeps the ball from falling straight down, so the ball causes the rod to pivot about the hinge. The ball falls along an arc of a circle whose center is A. The ball strikes the Earth at B.
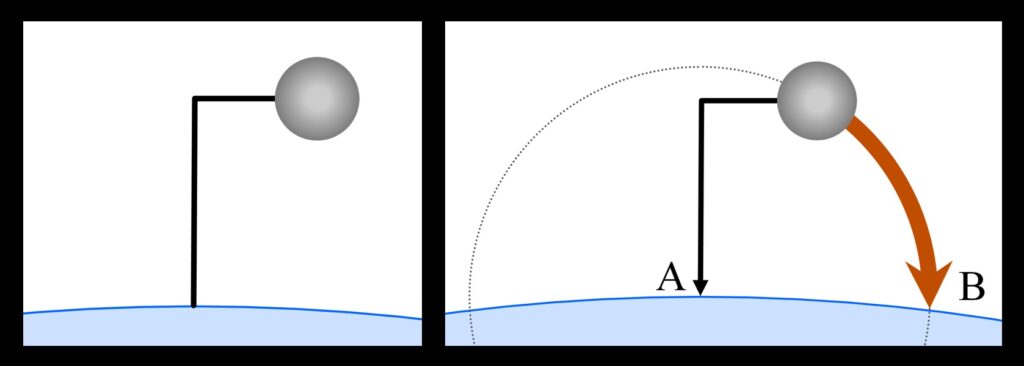Left—An iron ball attached to an L-shaped rod, buried in the Earth. Right—When the rod is hinged at Earth’s surface (A), the ball falls in a circular path and strikes the ground at B.Next, says Locher, imagine that the Earth is made smaller relative to the rod. The same thing still occurs—the rod pivots; the iron ball falls in a circular arc. If the Earth is imagined to be smaller still, the rod will be what hits the ground, not the ball, so the ball stops at its lowest possible point (C as shown in the figure below), but it still falls in a circular arc whose center is A. If the Earth is imagined to be progressively smaller, the ball still falls, driven by its gravity, in a circular arc.
The iron ball falls in a circular path, even as Earth is imagined to be smaller and smaller.At last Locher says to imagine the rod to be pivoting on the center of the universe itself—the Earth vanishing to a point. Surely, he says, in this situation, a complete and perpetual revolution will take place around that same pivot point A (fiet reuolutio integra & perpetua circa idem A). If the rod is put into motion, it will circle back around to its starting point, and continue on from there again, as before, “and so on into perpetuity.” You can see all this in the illustration that Locher made for Disquisitions, seen below. Curves MN, OP, and QR are the surface of the Earth, being imagined smaller and smaller. S is the iron ball. A is the center of the universe. Circle CHIC is the path of the orbiting ball.
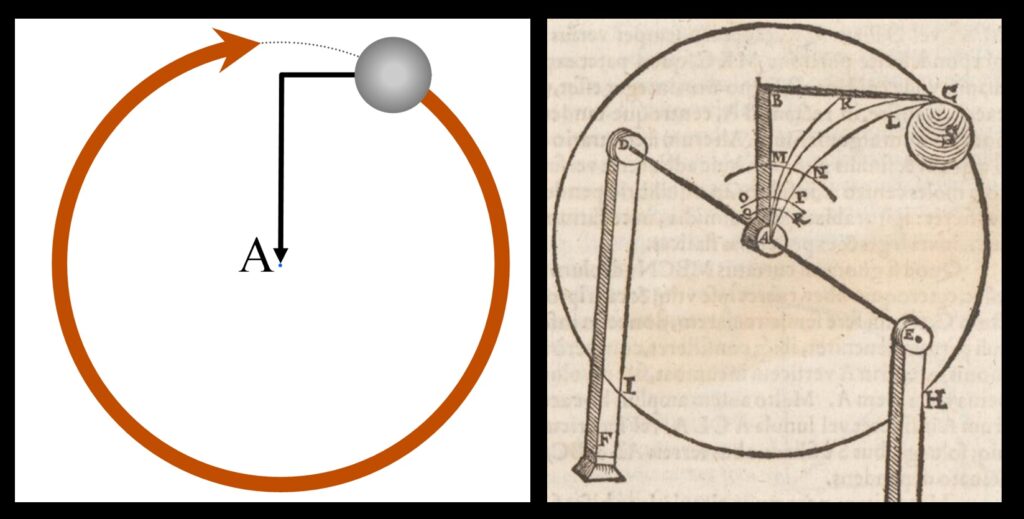Left—as Earth is imagined to shrink to a point, the ball swings in a circle around the Earth. Right—Locher’s diagram of this. Curves MN, OP, and QR are the surface of the Earth, imagined smaller and smaller. S is the iron ball. A is the center of the universe. Circle CHIC is the path of the orbiting ball.In this way, says Locher, we see that perpetual circular motion by a heavy body is possible. And if we imagine the Earth being in the place of the iron ball, suspended over the center of the universe, he says, now we have a thought experiment (cogitatione percipi possit—it may be able to be perceived by thought) that shows how the Earth might be made to revolve about that center, and therefore about the sun, which sits at the center of the universe in the Copernican world system. The Earth would revolve about the sun because it would be perpetually falling into the sun, in the same manner as the iron ball would be falling into Earth.
Now is that cool or what? That is, in my opinion, a very nice, clever, plausible, and understandable explanation of how an orbit might work.
Isaac Newton also explained orbits as a perpetual fall—some decades later. He explained orbits using a cannon ball launched from atop a mountain and falling to Earth. This is the explanation that students everywhere learn today in science class, and it is the explanation that you will hear on science shows like NOVA:
The idea that an orbit is a perpetual fall is the modern explanation for how things orbit. So, Locher’s discussion seems prescient. However, he himself attributed little weight to this idea. Even if such motion could actually occur, it would not help the Copernicans, he said, because it explains no observations.
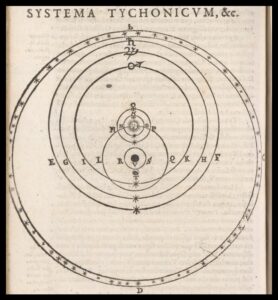
The system of Tycho Brahe, as illustrated in DisquisitionsLocher believed that the Earth was immobile at the center of the universe. He felt that observations of both astronomical and terrestrial phenomena supported an Earth-centered system, and opposed any motion of the Earth. He backed the system of Tycho Brahe, where the sun, moon, and stars circled an immobile Earth while the planets circled the sun—a system that was fully compatible with the new telescopic discoveries of the time, such as the phases of Venus and the moons of Jupiter. Indeed, Locher saw these discoveries as supporting the old geocentric ideas. For example, he saw moons going around Jupiter not as supporting the Copernican system, as Galileo did, but as supporting the old Ptolemaic concept of epicycles. To Locher, the moons going around Jupiter as Jupiter itself moved was proof of the ancient concept of epicycles—circles moving upon circles. Ptolemy had postulated the existence of epicycles, Locher said, in order to explain the visually observed motions of the planets. Now, however, “the optic tube has established… that the center of the motions of the Jovian satellites is Jupiter…. Therefore epicycles do exist in the heavens”. Locher also questioned at length how falling bodies could be observed to descend vertically on a rotating Earth, since different points on a rotating Earth all move at differing speeds. And he attacked the Copernicans for their views regarding the sizes of stars.
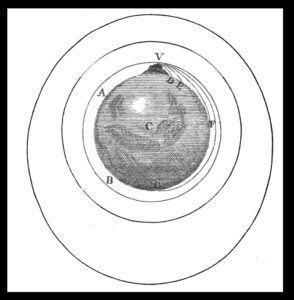
A star as seen through a very small aperture telescope, such as was used in the early seventeenth century (from J. F. W. Herschel’s 1828 Treatises on Physical Astronomy, Light and Sound). The globe-like appearance is entirely spurious, an artefact of optics (although this was not understood in Locher’s time) that makes the star appear vastly larger than it truly is. The vast sizes required for stars in the Copernican system in order for them both to show such size and to lie at such great distances that Earth’s motion around the sun produced no observable effects, was to Locher an argument for Earth’s immobility, and thus the Copernican system was to be rejected despite his physics explaining how Earth could orbit the sun.Even viewed through a telescope, stars were observed to have small but measurable disks, disks that in the first half of the seventeenth century were yet to be understood as spurious products of the optics of the telescope, and that did not represent the real bodies of the stars. Under the Copernican system, stars had to be so distant that by comparison the Earth’s orbit was like a point—immeasurably small, producing no observable effects. Locher noted that, since “small but measurable” is larger than “immeasurably small,” under the Copernican system every last visible star had to be larger than the Earth’s orbit. The Copernicans did not deny this, said Locher, but rather chalked up the giant stars to the power of God. Locher thought that was a “laughable” attempt to deal with the star size issue. In summary, Locher did not believe that his mechanism for explaining how Earth might orbit the sun could save the Copernican system from its flaws.
In 1651, Fr. Giovanni Battista Riccioli, an Italian Jesuit astronomer, dismissed Locher’s orbit mechanism. Riccioli was another Brahe-style geocentrist, and in his 1651 book Almagestum Novum, or New Almagest (referencing Ptolemy’s classic Almagest), he further developed the star size argument against Copernicus; he also went beyond questions about falling bodies and differing speeds on the surface of a rotating Earth, to develop arguments against Earth’s motion in which the modern reader will recognize the “Coriolis Effect”. But while Riccioli may have been of like mind with Locher on these matters, he dismissed the Disquisitions orbit mechanism in short fashion. Crediting Disquisitions to Scheiner, Riccioli wrote, “that most acute explorer of the sun hallucinates [hallucinatur]”. He did not grasp the thought experiment presented in Disquisitions. He only considered the final case of the ball orbiting a point. He omitted mention of the rod and ball standing on Earth’s surface and toppling, and his illustration of Locher’s diagram was very bare-bones. The idea of imagining the Earth to be smaller and smaller, and supposing that if the iron ball would naturally move in a circular path for an arbitrarily small Earth, then it would do so for a vanishingly small Earth, seems to have eluded him. Likewise a later Jesuit, Fr. Athanasius Kircher, included in his 1680 book Physiologia a bare-bones version of the orbit diagram from Disquisitions, along with an insultingly dismissive discussion. “Here I cannot disregard,” wrote Kircher, not mentioning Locher or Scheiner by name, “the vain fabrications and manifest paralogisms of some, which they believe—no, they assert—to demonstrate artificial perpetual motion to be able to be made by a sure way around the center of earth, and which they strive to show by this reasoning….” After providing a synopsis of the mechanism (a synopsis that again overlooked the concept of Earth being made smaller and smaller), Kircher continued, “I can hardly keep from laughing at the deceitful fallacies of the human imagination”. According to Kircher, this whole idea was the equivalent of saying that, were a trough built that encircled the globe, a ball would roll around it, or water would continually flow around it, forever.
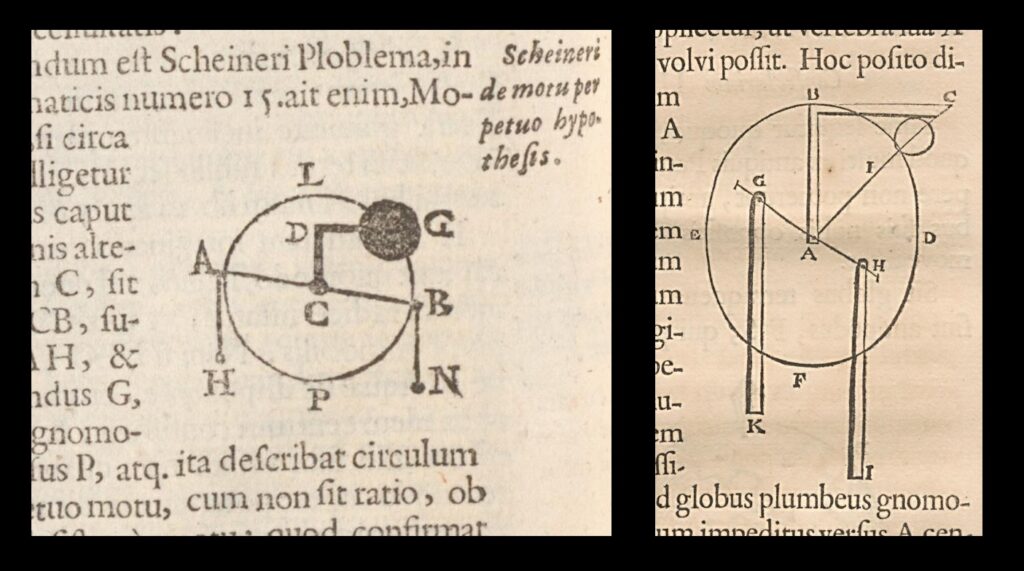Left—Riccioli’s version of Locher’s diagram. Right—Kircher’s version. Note how Frs. Riccioli and Kircher both show only the final outcome of Locher’s thought process—namely, the ball orbiting a point—and omit the circles that show the Earth being imagined to be progressively smaller.
Newton’s “Cannon on a mountain” illustration, from his 1728 A Treatise of the System of the World.By the time Fr. Kircher wrote this, Isaac Newton was already building the physics we now use. Unlike Locher and Scheiner, Newton departed from Aristotelian physics entirely, but he and they both agreed that an orbit is essentially a perpetual fall. So, you might wonder: did Newton ever encounter the ideas found in Disquisitions? Might he have even been inspired by them? There are hints to suggest that he might have encountered them, at least through Riccioli. Newton had a copy of the Almagestum Novum in his library. He and Robert Hooke exchanged letters in 1679-1680 regarding the easterly deflection that a heavy ball, suspended by a cord and then released, should exhibit were Earth rotating—one of the “Coriolis” arguments advanced by Riccioli against Earth’s rotation (the apparent absence of such deflection indicating Earth’s immobility to Riccioli). You can find the details on all this in Setting Aside All Authority (also by yours truly, also from the University of Notre Dame Press—click here).
Newton references Riccioli in his first edition of the Principia, the book in which he develops so much of his physics, but only in relation to the distance to the moon. Evidence that Newton ever encountered Disquisitions itself is difficult to turn up, and it seems doubtful that Riccioli’s perfunctory discussion of the Disquisitions orbit mechanism would have provided inspiration to anyone.
What happened to Locher after publishing his book? We do not know. Perhaps he died shortly after publishing Disquisitions. Perhaps he went off to missionary work in some far-flung place. Or, perhaps he went into charity work in a nearby place. He says in Disquisitions that he was from Munich. In the 1872 book Das Matrikelbuch der Universitæt Ingolstadt-Landshut-München under “Doctoren der Rechte” appears “Joh. Georg Locher, München [that is, Munich]” for 1617. The 1895 book Die Kunstdenkmale des Regierungsbezirkes Oberbayern notes a “Georg Locher, Waisenpfleger aus München”—a person who cares for orphans—as having in 1649 donated art to a certain church. All this plausibly could refer to the same Locher. If it is the same Locher (and that is a big “if”), then perhaps Locher found a calling in his own home town that was more important to him than science. Perhaps, sort of like Louis Sansbury, his strongest calling was to care for people in his community. We are deep in speculation here. However, it does not seem too speculative to suppose that, had he remained active in the scientific community, he might have developed his physics further. After all, he (with Fr. Scheiner) came up with the idea that an orbit is a perpetual fall.
The bottom line is this: The key idea of an orbit being a perpetual fall was proposed as early as 1614 by a Jesuit astronomer and his student. That idea circulated among knowledgeable readers. It came to the attention of and was discussed by two prominent Jesuit authors. However, the idea of an orbit as a perpetual fall was dismissed by those authors, and it had never been further developed by its originators. It would be proposed again by Isaac Newton, under a new physics, and would come to be the explanation that everyone learns in school of how an object remains in an orbit.
I am pleased to share all this with you, O Reader of The Catholic Astronomer. You will not have heard this story before, because it is all new research, just published in the Journal for the History of Astronomy in February 2019. In fact, this post is a modified version of the JHA paper. Click here to see the full published paper. Click here to see an early version of this story that I wrote as a guest post for The Renaissance Mathematicus blog back in 2016.
