This is a “re-run” of a post that originally ran on July 19, 2017.
My post for next week will feature Fr. Riccioli and the Coriolis Effect,
so revisiting this topic seems like a good idea.
Hurricane Sandy from 2012. Credit:NOAA.The Coriolis Effect is an apparent deflection of projectiles and falling bodies that is caused by the rotation of the Earth. It is named for Gaspard-Gustave de Coriolis, a French scientist who described it mathematically in the early 19th century. It is responsible for the rotation of weather patterns such as hurricanes. But it turns out that a century and a half before Coriolis did his work, other scientists were discussing the Coriolis Effect. These scientists were Jesuits—Fr. Giovanni Battista Riccioli, who discussed the effect in his 1651 book Almagestum Novum, and Fr. Claude François Milliet Dechales, who discussed the effect and included some nice simple diagrams of it in his 1674 book Cursus seu Mundus Mathematicae.
What is interesting about this is that Riccioli and Dechales were discussing an effect that they did not believe to exist. Their whole point was that, were Earth rotating like Copernicus says, that rotation would produce observable effects—deflection of projectiles and falling bodies. Since these effects are not observed, that is an argument against Copernicus, and in favor of an immobile Earth.
Now, they were wrong about the effect not existing. The effect exists, but it is much harder to observe than one might expect. Indeed, even Isaac Newton and Robert Hooke in 1679-1680 tried, without success, to use the effect to prove Earth’s rotation.
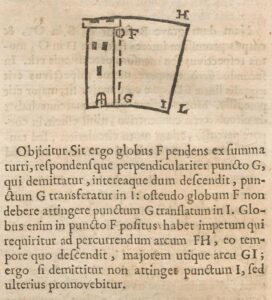Dechales’s tower illustration, from a 1690 edition of Cursus seu Mundus mathematicus. Click here for the entire page.How does the Coriolis Effect work? Well, let’s let Dechales explain it—he explains it well, using very clear illustrations. First the deflection of falling bodies:
A ball F, hanging from the top of a tower directly above point G, is dropped. While the ball descends, point G is carried [by Earth’s rotation] into I. I propose the ball F to be unable to arrive at point G (now at I). This is because the ball when positioned at F has a momentum [impetus] requisite for passing through arc FH (through which the tower top moves while the ball descends) which is greater than that requisite for arc GI. Therefore, if the ball is dropped, it will not arrive at point I, but will advance forward farther [to L].
Then, the deflection of projectiles:
Likewise, consider a cannon discharged in the direction of one of the poles [of the Earth]. During the time in which the ball would traverse the distance MO, the cannon [originally at M] would be carried to N, while the target [originally at O] would be carried to P. While the ball was at M, it had from the rotation of the Earth momentum able to carry it through arc MN (which is greater than arc OP) during the time required to travel from M to O. But the ball, separated from the cannon, conserves this momentum whole [totum hunc impetum conservat]. Therefore it should run through a distance greater than OP, and consequently not hit the target.
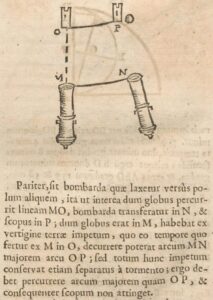 Dechales’s cannon illustration, from a 1690 edition of Cursus seu Mundus mathematicus. Click here for the entire page. |
 You can read all about this in this month’s issue of Physics Today! Just click here. |
Note how Dechales illustrates the cannon ball passing to the right of the target. For a more detailed discussion from the Cornell University ArXiv preprint server, click here.
