Photo from Notre Dame.
Photo from Notre Dame.Over time I have had the pleasure of introducing to readers of Sacred Space Astronomy guest bloggers who are scientists, bishops, and worship directors. Now I am pleased to introduce a mathematician. Jeffrey Diller is Professor of Mathematics at the University of Notre Dame (currently on leave, having finished up a term as chairperson of the Department of Mathematics there). He studies dynamical systems that arise in a complex analysis context. He also teaches: he was awarded the Fr. James L. Schilts, C.S.C./Doris and Eugene Leonard Teaching Award at Notre Dame in 2012, the Joyce/Kaneb Award for Undergraduate Teaching in 2015, 2008, and 2003.
Since I have been running a series of posts on the topic of mathematics, I wanted a mathematician to give a mathematician’ s perspective on what is great, and what is appealing, about mathematics. Jeff tells me that he became interested in the topic of this post in part out of his recent experience as coordinator for his kids’ middle school math club.
I have known Jeff since my freshman year in college (we shared a dorm room; I once won a cheap burger off him by checkmating his king on a specific square). He is the godfather of my younger son, and I am the godfather of his youngest son. He lives in South Bend, Indiana, with his wife and three sons.
Jeffrey Diller, 29 Jan 2020
The idea of cutting up and reassembling geometric figures for fun and profit goes way back in mathematics. For instance, there is my favorite argument for why the Theorem of Pythagoras is true. Here it is in purely pictorial form: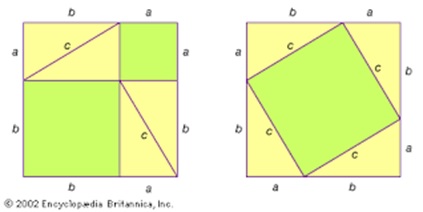
If this picture seems unfamiliar, then you owe it to yourself to spend a little time understanding what it says. This video might help:
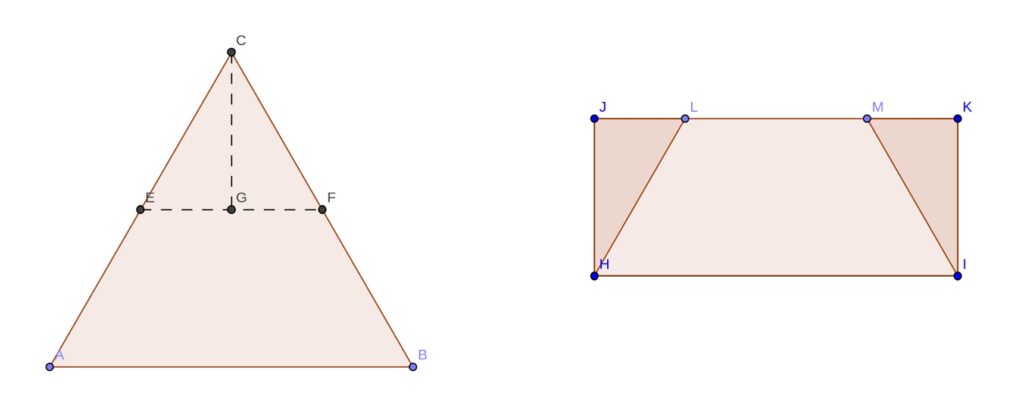
Done? Then let’s move on to related problem. I get out a piece of paper and draw on it an equilateral triangle (i.e. one where all three sides have the same length). Then I hand you the paper and a scissors and ask you to cut up the triangle, along straight lines only, and reassemble the pieces into a rectangle. Can you do it? In fact yes, by mountaintop removal, as illustrated by the next picture.
A substantially more difficult problem is to cut up the triangle into pieces that can be reassembled into a perfect square. This time I leave you to think about how, observing only that the square you get should have exactly the same area as the triangle you started with.
These are particular instances of what are known generally as ‘scissors congruences’. Recall that a polygon is a two dimensional plane figure whose edge is a finite collection of straight line segments. We say that one given polygon is scissors congruent to another if it can be cut up into smaller polygons which can then be reassembled into the second given polygon. It turns out that two polygons are scissors congruent as long as they have the same area, though it is somewhat challenging to explain how in general and even more so to figure out how few cuts one needs to turn one polygon into the other. If you’ve ever messed with ‘Tangram puzzles’ (below), then you have some experience with scissors congruences.
Any good problem is worth generalizing, so if you are of the mathematical persuasion you might wonder what happens when you go from polygons in the plane to flat-sided three dimensional shapes (polyhedra) in space. If two polyhedra have the same volume are they scissors (machete?) congruent? The eminent German mathematician David Hilbert raised this question around 1900 in a notorious list of notable unsolved problems. His student Max Dehn answered it a year later: a perfect cube cannot be dissected into polyhedral pieces that admit reassembly into a triangular pyramid with all sides equal (a regular tetrahedron)—even if the cube and the tetrahedron both have volume 1.
In a little more detail, what Dehn did was to first give a recipe for combining all the angles in any polyhedron into a sort of weighted total angle and then show that this total angle isn’t changed when you cut the polyhedron up into pieces and reassemble them. Finally, he computed the total angle for the cube and the tetrahedron and showed that they were different. QED…
More than half a century later, mathematicians complemented Dehn’s result by showing that when different three-dimensional polyhedra have the same volume and the same ‘Dehn total angle’, they must be scissors congruent. That is, there is no other obstacle, beyond volume and Dehn’s total angle, to cutting up one in order to turn it into the other. Later still, researchers established a similar fact about four dimensional shapes, even in spaces that are in some sense curved one way or another.
A simple geometry problem has turned out to be the entrance to a rabbit hole, and even after much exploring, we haven’t come close to mapping out the depths of it. Analogues of scissors congruence have have been developed and shown relevant for problems quite remote from plane polygons. Just this year, two young mathematicians, Jonathan Campbell and Inna Zakharevich, made substantial new progress in the subject (click here for an article about their work; click here for the work itself), tying scissors congruence to a vast theoretical edifice known as homotopy theory.
Mathematics is like this. Attention given to simple puzzles is rewarded with access to an entire universe, neither entirely apart from nor entirely like our everyday world. Often enough, mathematics has been profitably applied to solve practical problems. But beyond any application there is also the sense that accompanies each leap in our mathematical understanding, each moment when a previously vague intuition about a problem crystallizes into something palpable and logically inevitable, of “arriving home and knowing the place for the first time.”
This post is part of a series of posts on Pi, infinity, and other things mathematical. Click here for the series.