My post last week was about brilliant Sirius, which turns out to be a double star, comprised of a much brighter Sirius A, and a faint Sirius B. We saw how the motions of these stars, seen in the video below, told us that the Sirius system was 8.6 light years away, and had 20+ times the sun’s luminosity. The motion of Sirius B orbiting around Sirius A takes 50 years to complete. The video below shows a little more than two complete orbits of Sirius B about Sirius A, from approximately 2020 to approximately 2154. The video is a simulation, and presents what you would see if you had a very good telescope aimed at the exact same point in the sky for all that time.
If the telescope is instead aimed at Sirius A, then the motion of Sirius B becomes a textbook case of an orbit—Kepler’s laws of orbital motion in action, as can be seen in the next video. One of those laws says that the mass of an orbiting system is equal to the cube of the system’s average separation divided by the square of the period of the system’s orbital motion.
M = R3 / P2
Here the mass M is in solar masses, the period P is in years, and the separation R is in Astronomical Units or AU (one AU being the distance from the sun to the Earth).
The period is 50 years—that can be directly observed. The separation (between Sirius A and Sirius B) is simply measured by watching Sirius B’s motion and measuring it from one extreme of its orbit to the other (see figure below). This is measured to be about 68 millionths of a radian (see last week’s post for more on radians, triangles, and distances). The average separation is half this, or 34 millionths of a radian.
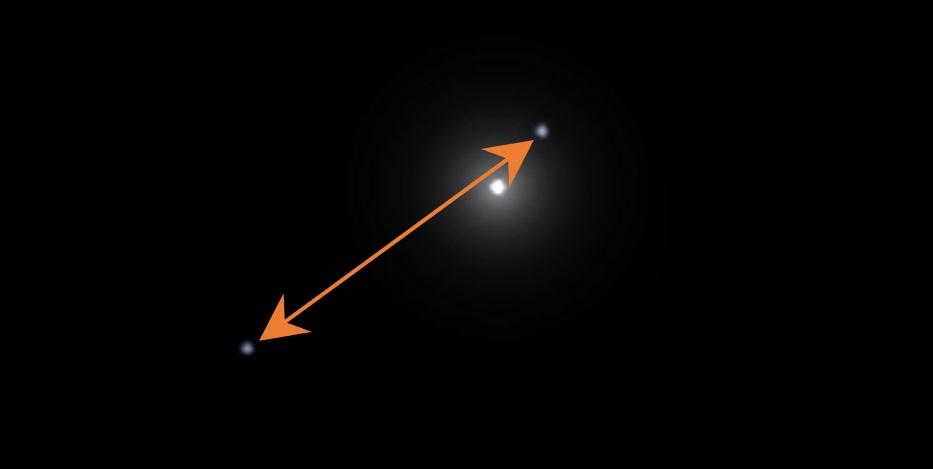This image shows Sirius B at approximately the two extremes of its orbit. The distance measures to be about 68 millionths of a radian.We calculated last week that the Sirius system is 0.5439 million AU away. So, using the same triangle math that we did last week, the average separation in AU is
R = 34 millionths of a radian x 0.5439 million AU = 34 x 0.5439 = 18.49 AU.
Now we calculate the mass of the system:
M = R3 / P2 = 18.493 / 502 = 2.5
So Sirius A and B together measure 2.5 times the mass of the sun. But how much is each star? Is that 2.5 solar masses split evenly between the two? Or does one have more mass than the other? We might expect that to be the case, since A is so much more luminous than B. Well, let’s take another look at the first video, but this time we’ll subtract out the looping effect caused by Earth’s own orbital motion.
The red mark is the barycenter of the system, the common point that both stars in fact orbit. Think of it as the balance point of the system. Note that at any given instant, Sirius B is always about twice as far from the barycenter as Sirius A. If we use the balance analogy, thinking of B and A like two kids on a teeter-totter, Sirius B is about half the mass of Sirius A. So, let’s logic this out.
Sirius B mass + Sirius A mass = 2.5 solar masses
But Sirius A is 2 of Sirius B so
Sirius B mass + 2 Sirius B masses = 3 Sirius B masses = 2.5 solar masses
Sirius B mass = 2.5/3 solar masses = 0.833 solar masses
And then since A is twice B, Sirius A has mass of
2 x 0.833 solar masses = 1.67 solar masses
So now we have the masses of the two bodies. In fact, this was a rough calculation. If you study the orbits of the two stars carefully, you see that they are tilted a bit with respect to Earth, and the tilt at which the orbits are seen alters their shape somewhat, as seen in the last video below. That would change that 68 millionths of a radian measurement above. We could, and really should, do that study of the orbits. However, the “correct” masses of Sirius A and B are in fact 2.0 solar masses for A and 1.0 for B—so our rough calculation is not so far off. Thus we will stop our Sirius business here.
Here you see how we know stuff about stars. From the colors of the stars we can get their temperatures, etc. as discussed in the post of two weeks ago. The way we come to know stuff about stars is we do the observations, and we do the math. After all, we can’t go measure the Sirius system with a tape measure and weigh it with a bathroom scale!
