Let’s take another look at Johannes Kepler and at Nibiru, the supposed planet that supposedly will wreak havoc on Earth in October. This is my second Nibiru post on this blog, the first being a couple of months ago. As I mentioned then, some people find this Nibiru business to be a lark, or just an example of the worst sort of internet misinformation. Others take it seriously—or don’t know how they are supposed to be able to know what to believe. But here at The Catholic Astronomer, Nibiru is a great opportunity to talk about how the solar system works, and about Johannes Kepler, the first astronomer to really figure out how the solar system works.
The Washington Post asked “Will the mysterious shadow planet Nibiru obliterate Earth in October?” They answered “No”, but no one need take their word for it, or anyone else’s. A person can reason this out for himself or herself, with a little help from Mr. Kepler.
In the previous Nibiru post we looked at the issue of the God-given harmony that the deeply religious Kepler saw in the solar system. This harmony is wholly incompatible with a wrecking ball plowing through every 3600 years like Nibiru is supposed to do. Modern scientists tend not to use words like harmony, so a more modern-sounding explanation might state this in terms of the dynamics of the solar system being incompatible with the existence of a Nibiru.
But consider another Kepler-based approach to Nibiru. Recall from both a recent post on Kepler and the last Nibiru post how Kepler discovered that in a system of orbits there is a linear relationship between the squares of the orbital periods and the cubes of the orbital distances. We saw this in the following table showing the distances of Venus, Earth, and Mars from the sun (all measured in terms of Earth’s distance), and the orbital periods of these bodies (all measured in years).
| Distance | Period | |
| Venus | 0.723 | 0.615 |
| Earth | 1.000 | 1.000 |
| Mars | 1.524 | 1.881 |
We took each period value and squared it—
0.615 x 0.615 = 0.38
1.000 x 1.000 = 1.00
1.881 x 1.881 = 3.54
—and each distance value and cubed it—
0.723 x 0.723 x 0.723 = 0.38
1.000 x 1.000 x 1.000 = 1.00
1.524 x 1.524 x 1.524 = 3.54
—and the linear relationship was obvious (harmony!).
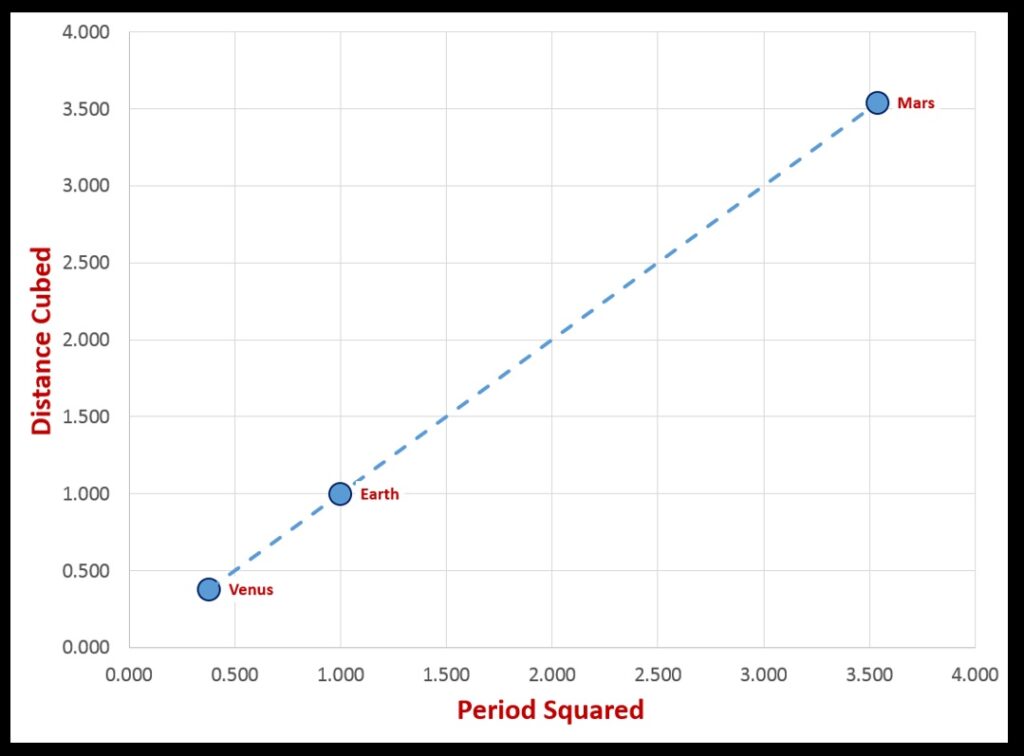 The linear relationship between the squares of periods and the cubes of distances for Venus, Earth, and Mars.
The linear relationship between the squares of periods and the cubes of distances for Venus, Earth, and Mars.Let us now use Kepler’s ideas on Nibiru. Its period is supposedly 3600 years (one reader of this blog sent me information claiming the last pass of Nibiru was responsible for Noah’s flood).
Let’s now square that period:
3600 x 3600 = 12,960,000
Now, to find distance, we need to know what value, when cubed, gives 12,960,000? The answer is the cube root of 12,960,000. And, thanks to a trusty calculator, I find that to be 234.8920585. We’ll cube that, just to be sure:
234.8920585 x 234.8920585 x 234.8920585 = 12,960,000
It works. Rounding 234.8920585 to 235, we can say the distance of Nibiru from the sun must be about 235 times the distance of Earth from the sun. The distance of Earth from the sun is called an Astronomical Unit or AU. The distance from one end of Nibiru’s orbit to the other will be 2 x 235 = 470 AU.
Kepler showed that orbits are elliptical. A circle is a special kind of ellipse, so circular orbits are elliptical orbits. As mentioned in the prior Nibiru post, the orbits of the planets are close to being circular.
If Nibiru was in anything like a circular orbit, it would always be about 235 AU away from the sun. Therefore it could never come close to Earth. And therefore it could never “obliterate Earth in October”.
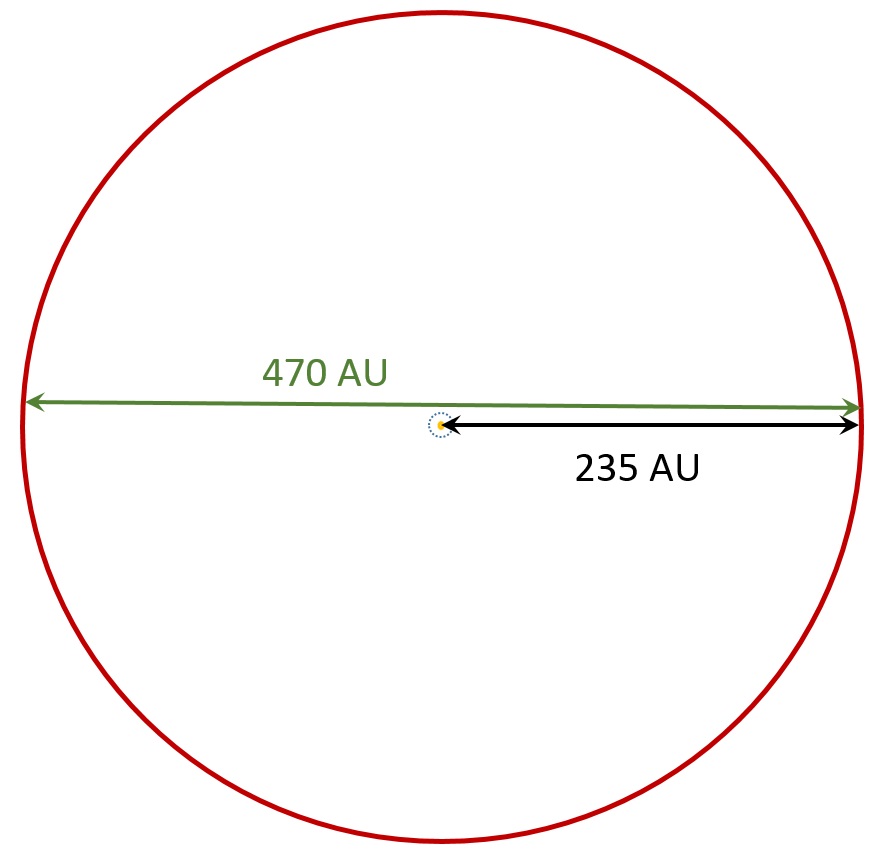 Nibiru in a low-eccentricity orbit. The sun is the yellow dot at center. The Earth’s orbit is the blue dotted circle. In this orbit Nibiru does not come close to Earth. This is not exactly to scale—the diameter of Earth’s orbit is only 2 AU, so Earth’s orbit should be smaller.
Nibiru in a low-eccentricity orbit. The sun is the yellow dot at center. The Earth’s orbit is the blue dotted circle. In this orbit Nibiru does not come close to Earth. This is not exactly to scale—the diameter of Earth’s orbit is only 2 AU, so Earth’s orbit should be smaller.But there are many ways to be an ellipse. All of the shapes below are elliptical. All measure the same in terms of distance from one end to the other. The skinny elliptical orbits are said to have high eccentricity; the more circular ones are said to have low eccentricity.
There are plenty of objects in the solar system that have high-eccentricity orbits. Many of these objects are comets, as seen below.
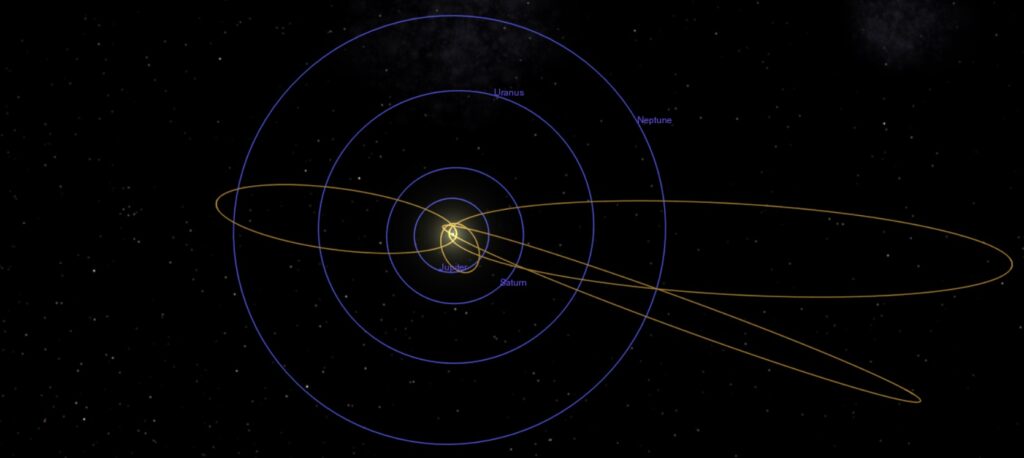 The blue orbits are the low-eccentricity orbits of planets. The gold orbits are the high-eccentricity orbits of comets.
The blue orbits are the low-eccentricity orbits of planets. The gold orbits are the high-eccentricity orbits of comets.Note that in high-eccentricity orbits, the Sun is located near one end of the orbit. This has to do with the mathematics of ellipses and their focus points. Kepler showed that the Sun is located at an orbit’s focus. That focus is near the center of the ellipse in a low-eccentricity orbit, but near the end in a high-eccentricity orbit.
So, now we understand how Nibiru can (supposedly) have a 3600 year period and still “obliterate Earth in October”: it must be in a high-eccentricity orbit that causes it to sweep in close to the sun, where it can wreak havoc on Earth. The length of that orbit will be 470 AU. The average distance of Nibiru from the sun, the value that is important in Kepler’s “period squared is proportional to distance cubed” rule, remains 235 AU.
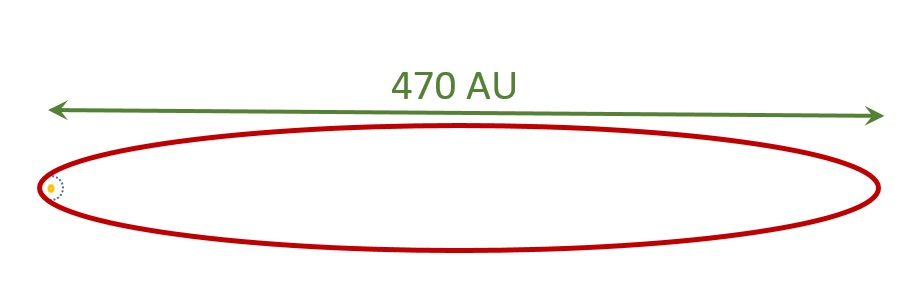 Nibiru in a high-eccentricity orbit. The sun is the yellow dot at the left end. The Earth’s orbit is the blue dotted circle. Here Nibiru comes close to Earth once per orbit. This is not exactly to scale—the diameter of Earth’s orbit is only 2 AU, so Earth’s orbit should be smaller.
Nibiru in a high-eccentricity orbit. The sun is the yellow dot at the left end. The Earth’s orbit is the blue dotted circle. Here Nibiru comes close to Earth once per orbit. This is not exactly to scale—the diameter of Earth’s orbit is only 2 AU, so Earth’s orbit should be smaller.Based on this high-eccentricity orbit, we can reason out how fast Nibiru should be moving when it sweeps in close, where it should be at different times, and even where it should be visible in the sky! All this based on what we’ve done so far!
First, let us suppose that Nibiru sweeps in so that its distance of closest approach to the sun is 1 AU. This is the distance that would make it most likely for Nibiru to hit Earth or come close enough to Earth to disrupt life on Earth. Why? Because, Nibiru’s orbit will run with Earth’s for a while, providing lots of chance for Nibiru and Earth to meet.
It turns out that in a big, high-eccentricity orbit like the one Nibiru must have in order to both have a period of 3600 years and hit the Earth, the speed at the point of closest approach to the sun (that is, the speed at perihelion) is approximately the same as the escape velocity from the sun at that point (escape velocity is the velocity required for an object to completely escape the gravitational pull of another object). Why is this true? Reason it out this way: Imagine that Nibiru does not encounter Earth as it sweeps around the sun in its orbit. Nibiru’s velocity is such that it will head back out on its orbit, out to 470 AU, to return in another 3600 years. Gravity gets weaker with distance. At 470 AU the sun’s gravitation pull is weak. Because it is so weak at that point, the speed needed to sail out to 470 AU and return in 3600 years is not much less than the speed needed to sail out to 470 AU and just keep going and never return (that is, to escape). So Nibiru’s perihelion speed is just slightly less than its escape velocity.
 Orbital velocity is “17,544 miles per hour“.
Orbital velocity is “17,544 miles per hour“.And escape velocity is roughly 40% greater than the circular orbit speed at that same distance. For example, the speed of a satellite in a low circular orbit around Earth is about 17,500 mph (a number that pops up in the movie Hidden Figures). 40% of 17,700 mph is 0.40 x 17,500 = 7,000 mph. And 17,500 + 7,000 = 24,500 mph, approximately 25,000 mph, which is indeed the escape velocity from Earth.
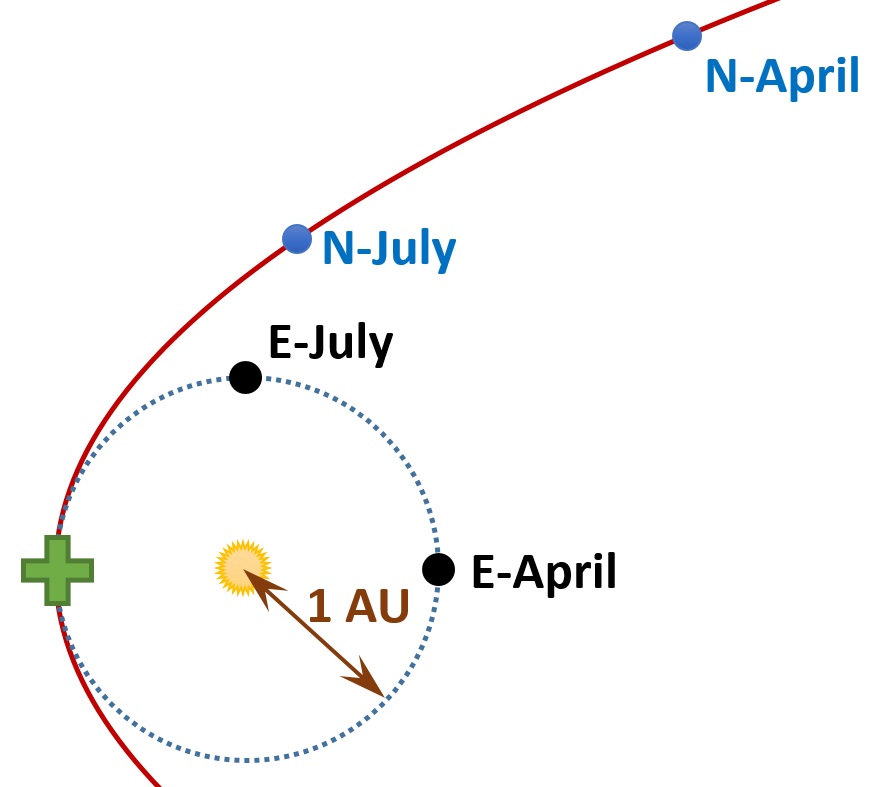
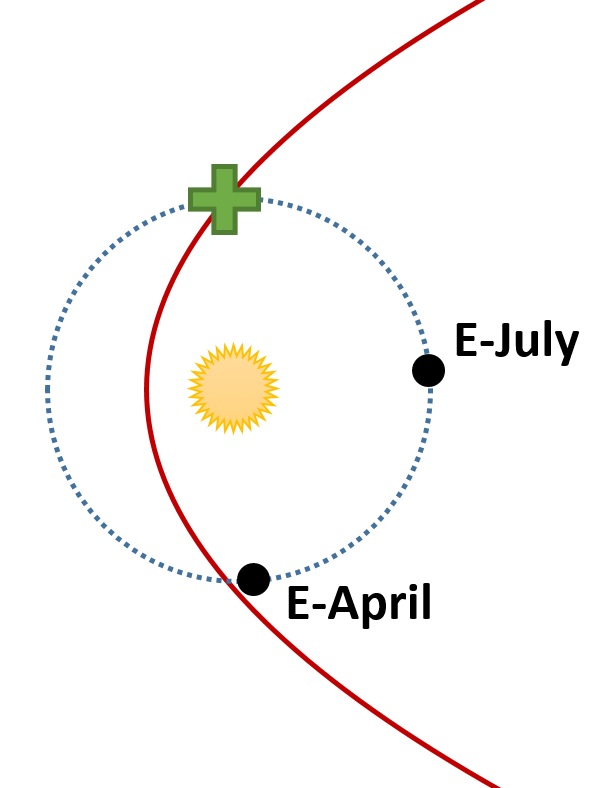
Now, this post is appearing on July 5. October is merely 3 months away. Three months is a quarter of a year, so Earth right now (labelled “E-July” in the figure below) is one quarter of an orbit from the point of encounter with Nibiru (that point is marked with a +).
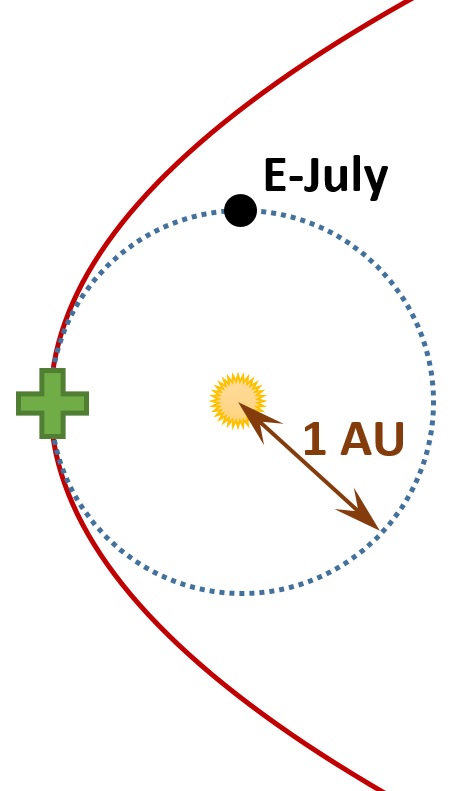 Shown here are the sun, the supposed orbit of Nibiru (red line), the Earth’s orbit, and the Earth. Earth moves counterclockwise in this figure. The Earth’s location shows where it is now in July. Nibiru will supposedly hit or otherwise encounter Earth in October, which is 3 months, or 1/4 of a year, from now. The point where Earth and Nibiru will supposedly meet, which is 1/4 of the way around Earth’s orbit from where Earth is now, is marked with a +.
Shown here are the sun, the supposed orbit of Nibiru (red line), the Earth’s orbit, and the Earth. Earth moves counterclockwise in this figure. The Earth’s location shows where it is now in July. Nibiru will supposedly hit or otherwise encounter Earth in October, which is 3 months, or 1/4 of a year, from now. The point where Earth and Nibiru will supposedly meet, which is 1/4 of the way around Earth’s orbit from where Earth is now, is marked with a +.Now, all eight known planets in the solar system orbit in the same direction around the sun. Let us suppose that Nibiru does the same. Earth is orbiting counter-clockwise in the figure below, so Nibiru would be, too. If Nibiru is moving 40% faster than Earth, then Nibiru right now must be 40% farther from the +, and of course on its orbit. That works out to Nibiru supposedly being in about the location shown below.
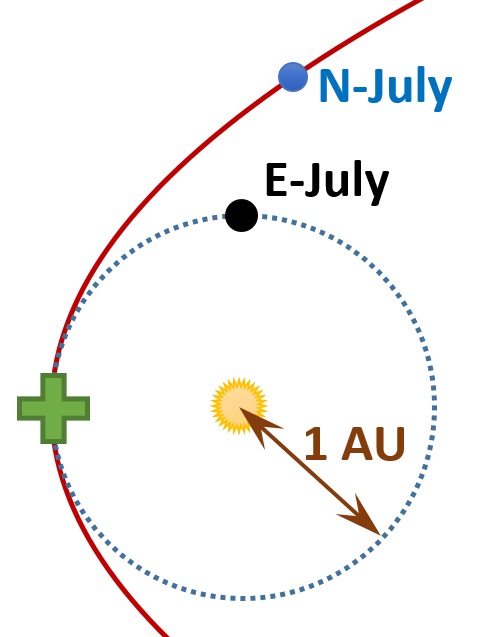 Nibiru’s supposed location right now (marked “N-July”), based on it being 40% farther from the + point along its orbit than Earth is along its orbit.
Nibiru’s supposed location right now (marked “N-July”), based on it being 40% farther from the + point along its orbit than Earth is along its orbit.Look carefully at the above figure. Note first that Nibiru should be opposite the sun in the sky. In other words, Nibiru should be visible at night. When the sun goes down, Nibiru should be up. Note second that Nibiru right now should be darned close to Earth—about 1 AU or less. Do you recall seeing Mars in the evening sky after sunset back in March? Back then Mars was over 2 AU distant from Earth, and it was plenty bright. Nibiru should be a naked-eye object that is much more obvious now than Mars was then.
 Mars and Venus the night of March 2, 2017. (Venus is the bright object above the ‘W’, and Mars is to the upper left of Venus.) Mars was about 2.1 AU distant. Note that it was as bright as the belt stars in the constellation Orion (visible at upper left).
Mars and Venus the night of March 2, 2017. (Venus is the bright object above the ‘W’, and Mars is to the upper left of Venus.) Mars was about 2.1 AU distant. Note that it was as bright as the belt stars in the constellation Orion (visible at upper left).Moreover, Nibiru should have been visible for the past several months. Let’s go back three months to April 5, another 1/4 of an orbit ago. Earth would be opposite the + mark, at “E-April”. Nibiru, moving 40% farther than Earth in those same three months, would be in the location “N-April” shown below. Note that in April Nibiru would still have been only a few AU from Earth. It would have been plenty bright. Tonight (July 5) Jupiter’s moon Ganymede is bright enough that, were Jupiter’s glare not overwhelming it, it would be visible to the naked eye. Ganymede would be smallish for a planet, and it is currently over 5 AU from Earth! Also note that Nibiru would have been more than 90 degrees from the sun in the sky, and thus visible for a good portion of the night. Moreover, between April and now Nibiru could never have been on the same side of Earth as the sun was. Thus claims that “Nibiru can’t be seen because it is on the other side of the sun” can’t be true (unless Nibiru is not a planet but rather a magical body that does not obey the physics of orbits).
If we assume Nibiru is orbiting in the opposite direction as the rest of the planets, the situation is not much different. The positions would be as shown below. Right now Nibiru would be about to briefly disappear behind the sun, only to reappear on the other side and rapidly close with Earth, but for the past three months Nibiru should have been easily visible to the naked eye, in the night sky.
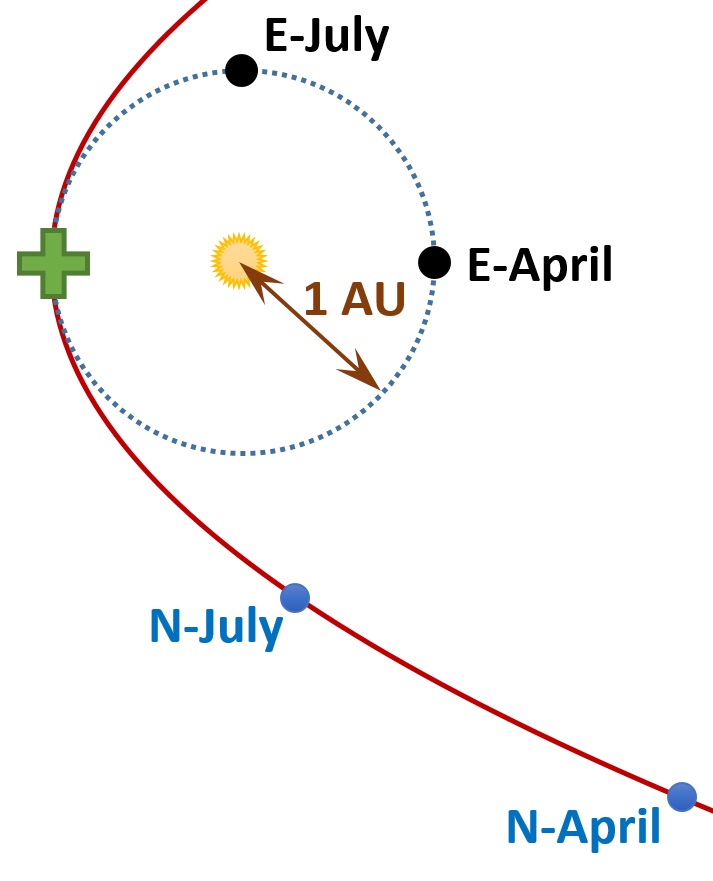 The supposed positions of Earth and Nibiru in July and April if Nibiru is orbiting in the opposite direction as Earth.
The supposed positions of Earth and Nibiru in July and April if Nibiru is orbiting in the opposite direction as Earth.So, in the last Nibiru post we saw that the idea of Nibiru was contrary to what Kepler discovered about the nature of the solar system. In this post we have found that the idea of Nibiru is contrary to what Kepler’s discoveries, a little reasoning, and our own two eyes tell us. There is no Nibiru. It is as reasonable to suppose that Earth will be destroyed in October by the evil wizard Voldemort as it is to suppose that Earth will be obliterated by the non-existent Nibiru. I’m now looking for the headline that reads “Will Voldemort destroy Earth in October?”
 Changing Nibiru’s orbit does not change the overall picture. If the perihelion point is outside Earth’s orbit, then Nibiru won’t reach Earth. If the perihelion point is inside, as seen here, then while Nibiru might move faster when inside Earth’s orbit, the speed outside is not changed, and any interaction or collision with Earth can only occur at two points. And Nibiru still will have been visible and bright for the past few months.
Changing Nibiru’s orbit does not change the overall picture. If the perihelion point is outside Earth’s orbit, then Nibiru won’t reach Earth. If the perihelion point is inside, as seen here, then while Nibiru might move faster when inside Earth’s orbit, the speed outside is not changed, and any interaction or collision with Earth can only occur at two points. And Nibiru still will have been visible and bright for the past few months.Nibiru might be a bunch of nonsense, but it provides a great excuse to illustrate all the things we can learn about orbits with just some very basic knowledge. Look at all we could figure out! And we did not use calculus, or crunch numbers on a computer! This sort of thinking and testing and working our way toward the truth is what science is.