Randomness is a popular concept. People invoke it as an explanation for the world: stuff just happens. No explanation or cause needed. The world has chaos in it.
Consider the throw of a pair of dice (or the spin of a cake wheel). Dice sure seem random, like something that “just happens”. Indeed, since human beings cannot calculate how dice will fall, many people have attributed such “chance” events to divine will, and have viewed games of chance as dragging divine action into trivial matters; thus the games were considered to be inherently blasphemous.
But in the last century, science learned something about chance events. Scientists using computer models for weather forecasting found that something as regular and predictable as a mathematical formula could yield seemingly “random” results. This was not because there was any true chaos in the math (math by its nature cannot be random: 2+2 is always 4). Rather, it was because the math in the weather model was highly sensitive to slight changes. Tell the model today’s high is 88.0 degrees, and it might predict rain for two weeks from now; but tell it 88.1 degrees and it might predict sunshine. This became known as “The Butterfly Effect”, for even if scientists had a perfect understanding of how the weather worked, they could never forecast it well, because they could never account for the flap of every butterfly’s wings that might slightly change the inputs.
This is how it is with dice, too. We understand all the physics of dice. We understand how dice work. But dice are highly sensitive to inputs—to exactly how they are thrown, to every tiny bump on the surface to which they fall—so how they come up cannot be predicted. Dice seem “random” to us because we cannot know all the inputs. If we could, we would know exactly how they would come up, every time.
Dice then look random, but in fact their behavior is determined by simple laws of physics. The term for this is “deterministic chaos”. We just do not know enough to predict how dice will come up.
(In computer games or other simulations, by the way, how dice will come up can be known. If you know the mathematical algorithm that was written to control the simulated dice, you can know exactly how they will come up, every time. This is why numbers in the lottery are generated with those balls, not with a computer.)
All “random” things are like dice in some way. Modern science views nothing in the universe as being random—as being lawless chaos, stuff that “just happens”. Science is based on the idea that the universe can be understood, that it follows knowable laws. Lawless chaos could not be understood and could not be studied by science. Some things in science may seem random. The decay of a nucleus of an atom of radioactive material, for example, exactly mimics the roll of a die. But we have no reason to believe that radioactive nuclei are any more random than dice are.
The astronomer and historian of science Agnes Mary Clerke wrote in her 1903 book Problems in Astrophysics that science asserts that “there is no such thing as chaos…. for chaos is the negation of law, and law is the expression of the Will of God.” Or as the hymn “Praise the Lord! Ye Heavens Adore Him” (based on Psalm 148) says, “laws that never shall be broken for their guidance He has made”. For the guidance of everything, it seems. Nothing “just happens”.

There is an interesting artistic interpretation of all this in the floor of the church at St. Meinrad Archabbey in Indiana. The floor features both regular triangles and seemingly random bits of flooring. According to the book, To Prefer Nothing to Christ: St. Meinrad Archabbey 1854-2004 (Abbey Press, St. Meinrad, Indiana, 2004), the design for the floor represents a modern interpretation of a medieval and Renaissance tradition of floor designs:
With its stunning design of triangles (suggesting the Trinity) and curved lines, the floor patterns were developed by Ben Nicholson, a specialist in medieval and Renaissance floors, and the chief architect, Evans Woollen, of Woollen, Molsan and Partners of Indianapolis [Indiana, USA]. Nicholson, aware that the geometry of medieval and Renaissance floors gave expression to philosophical and theological ideas, wanted to make a modern theological statement. Therefore, he drew on his understanding of “chaos theory”, which argues that order underlies phenomena that appear to be random and chaotic. Thus, the broken marble in the side aisles suggests chaos, which moves toward the elaborate designs of Sierpinski’s triangle in the center of the circles. For Nicholson, the movement from randomness to design, from chaos to order, is a statement about God and the universe.
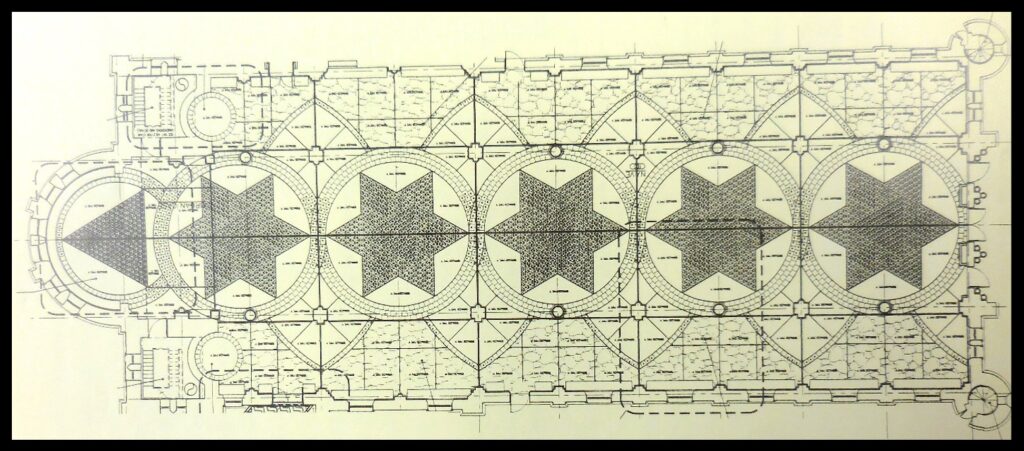
Sierpinski’s triangle is a geometrical shape in which an equilateral triangle has another equilateral triangle inscribed within it, forming more triangles, which then have triangles inscribed within them, and so on indefinitely. Shapes like this, which look the same at whatever scale you look at them (you can magnify Sierpinski’s triangle as much as you want, and you see the same thing), are said to be “fractal” in form. Graphical representations of mathematical formulas that yield deterministic chaos tend to be fractal in form. Below are animations of a Sierpinski’s triangle and a Sierpinski triangle transformed into a fractal tree.





Click here for other posts related to St. Meinrad Archabbey.

