In The Gravity of Math: How Geometry Rules the Universe (New York: Basic Books-Hatchette Book Group, 2024), Steve Nadis and Shing-Tung Yau take readers on a historical trek through the mathematics behind Einstein’s Theory of Relativity. What strikes me about the book is not its treatment of its main subject (to my mind that treatment lacks the non-mathematical explanations needed for the general reader, while also lacking the full mathematical connections needed for the more knowledgeable reader) but what it has to say about math itself. Nadis is a science writer, whereas Yau is a mathematician of great accomplishment: Professor Emeritus at Harvard (now at Tsinghua University) and a recipient of the Fields Medal (the mathematician’s “Nobel Prize”, in a sense), the National Medal of Science, and a MacArthur Fellowship. Therefore, I tend to attribute what the book says about math to Yau.
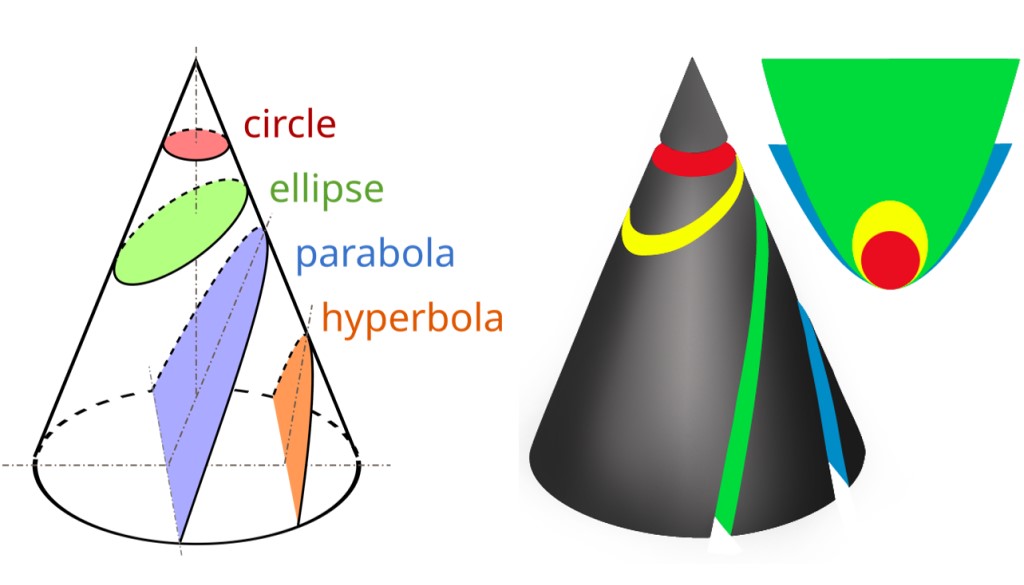
The book’s prelude talks about the Greek mathematician Apollonius of Perga, who lived 200 years before Christ. Known in his time as “The Great Geometer”, Apollonius wrote on conic sections (an eight-volume series he called Conics). Conic sections are the shapes that result from slicing a cone with a plane: circles, ellipses, parabolas, and hyperbolas. Nadis and Yau write that Apollonius’s work “lay essentially dormant” for 1800 years, until Johannes Kepler came along and figured out that the orbit of Mars is an ellipse. Now Apollonius’s work is strongly tied to astronomy: The orbit of Venus is indistinguishable to the eye from a “perfect circle”; the orbits of Mars and Mercury are more obviously elliptical; the orbits of comets are highly elliptical and can be parabolic; the trajectory of a NASA probe whizzing through the Jovian system on its way to the outer solar system is hyperbolic.

A central point of The Gravity of Math is that Albert Einstein also dug up some neglected math for his Theory of Relativity. The authors write (page 6):
It bears repeating that this wildly successful and productive theory [of Relativity] was built around a bit of mathematics — a form of geometry — that had been largely ignored by physicists for nearly half a century. In crafting his laws of planetary motion, Kepler similarly drew upon an 1,800-year-old treatise on conic sections … which had not, until then, had much impact on physics at all.
And here Nadis and Yau get interesting, and almost theological:
This, of course, speaks to the incredible staying power of mathematics. A rigorously proved mathematical theorem has the property — rare, if not unparalleled in human affairs — that it will hold up for all time. These axioms of eternal truth (to paraphrase Thomas Jefferson) represent tools, of sorts, that can be rediscovered later — even centuries later — and used in ways that [their] authors never dreamed of.
“All time” … “eternal truth”. What are Nadis and Yau getting at here? Toward the end of the book, Yau goes solo, writing a poetic “Ode to Geometry”. He begins with,
The bounty of heaven, so vast and beautiful.
Who could not but marvel at its miraculous display?
Further on in the “Ode”, Yau touches on how falling apples and elliptical orbits “all reduce to the union of space and time and the myriad ways it can bend”. He then touches on “the violent, infinite warping of ravenous black holes”, and from there proceeds to conclude the “Ode”:
These seemingly inscrutable objects, enigmatic, shrouded in darkness,
reveal their secrets, in time, through the unyielding power of
geometry.
Honed over the centuries and enduring for millennia,
these tools, and their associated theorems, have never let us down.
Truth is elusive, defying the best minds that history has produced.
Yet a simple mathematical proof can guide us, inexorably, to the
eternal.
I have long found that one of the most compelling non-religious arguments that human beings are more than mere evolved, finite “bags of mostly water” (one of my favorite Star Trek phrases) with chemistry going on in them is this: that humans can conceive of, and deal in, the eternal, the infinite and the perfect — things we have no experience with and could not have evolved to grasp; things “unparalleled in human affairs”. It sure seems like Shing-Tung Yau is driving at something like that argument.