Last fall, National Geographic published a new book by Neil deGrasse Tyson and Lindsey Nyx Walker, called To Infinity and Beyond: A Journey of Cosmic Discovery. The following appears on the first page of the first chapter of that book:
For thousands of years, humans reasonably assumed the Moon to be a flat disk of light that waxed and waned — until the 17th century, when Galileo Galilei dared turn his freshly perfected telescope skyward, revealing a textured sphere…
This statement is clearly wrong. The moon does not look like a flat disk. It looks like an illuminated sphere. In all likelihood, people grasped that the moon was a sphere the moment someone looked at a spherical rock or piece of fruit illuminated by a fire and noticed that its appearance when seen from different angles was moon-like. It was not reasonable to think the moon was flat.
Aristotle wrote, “the evidence of our eyes shows us that the moon is spherical”. Aristotle lived roughly two thousand years before the invention of the telescope. He wrote this in his On the Heavens (Book 2, Part 11). He continued, “For how else should the moon as it waxes and wanes show for the most part a crescent-shaped or gibbous figure, and only at one moment a half-moon?”
Aristarchus, who lived a century after Aristotle, calculated the distance to the sun based on the moon being a sphere illuminated by the sun. He did this using only the human eye and a tool for measuring angles — a protractor. He determined what the angle between the sun and the moon is at the point when moon appears to be exactly half illuminated as seen from Earth. Aristarchus thought this angle was at least 87 degrees.
Next, he kept in mind that, if the moon is a sphere lit by the sun, and the moon appears half illuminated, then the angle between the Earth, moon, and sun is 90 degrees, as shown in the following rough sketch:
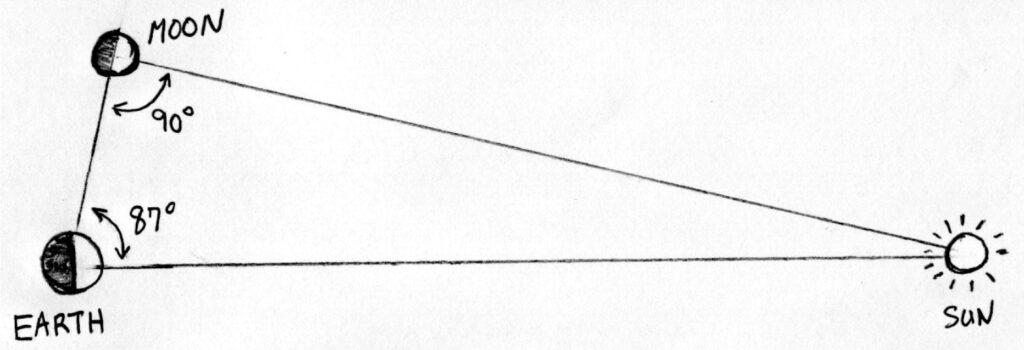
If you draw a precise triangle where one angle is 87 degrees and the other is 90 degrees, and measure the sides carefully, you will find that for an angle of 87 degrees, the sun turns out to be 19 times more distant from the Earth than the moon (you can also determine this using a trigonometric function). The triangle in the sketch below is drawn with precision. If you measure the distance E-S you will find it is 19 times greater than the distance E-M.

It is very hard to determine exactly when the moon appears to be exactly half illuminated. Aristarchus’s 87 degree figure is not quite right. In fact, the answer is more like 89.9 degrees. The triangle is far longer and skinnier than the one above. But Aristarchus did make the important determination that the sun was much more distant than the moon. The idea that the moon is an illuminated sphere was important to that determination.
As an historian of astronomy, this error in To Infinity and Beyond bothers me. Plenty of people will read that book for reason of the Tyson and National Geographic names alone. They may not read all of the book, but they will all read enough of it to learn the misinformation that everyone thought the moon was a flat disk until the telescope came along.
Correct information matters. We are awash in misinformation today. We do not need reputable names contributing to the problem.
Well, I am not just complaining about this. I wrote to the authors and publisher, asking them how such an error gets into print, to be associated with names like Tyson and National Geographic. I invited them to elaborate; a lengthy discussion will not bore me, I told them.
I will let you know if I hear anything.

