This post is based on a series of four posts that originally appeared here in July of 2016.
My posts for the next two weeks will be on the science of learning about the stars through “double stars”, so this is good material to “re-run”.
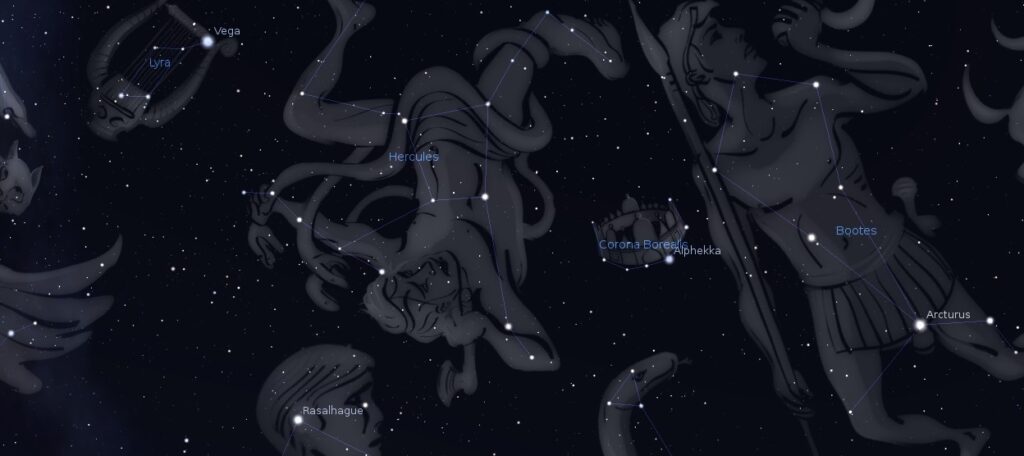
Look up at the summer night sky. You see stars, of course. There are bright stars like Vega and Arcturus, middling stars like Polaris (the North Star) and Mizar (the star in the “bend” of the Big Dipper’s handle), and faint stars like Rho Leo (an unremarkable star in the constellation of Leo, the lion) and Alcor (the dim companion of Mizar). When we look at these stars, what are we seeing? How do we know what the stars are? You have probably heard that the sun is a star, but are all these stars suns?
Some of the stars of the summer sky as represented by the Stellarium planetarium app.I have previously discussed in this blog how a person with excellent vision will see stars as small, round dots of differing apparent sizes, or magnitudes. Magnitude means bigness, as this old discussion of the scale of magnitudes indicates:
The fixed Stars appear to be of different Bignesses…. Hence arise the Distribution of Stars, according to their Order and Dignity, into Classes; the first Class… are called Stars of the first Magnitude; those that are next to them, are Stars of the second Magnitude… and so forth, ‘till we come to the Stars of the sixth Magnitude, which comprehend the smallest Stars that can be discerned with the bare Eye….
The idea of magnitude as bigness also shows clearly in this old discussion of the changing magnitude of a “new star” or “nova”:
…from the sixteenth to the twenty-seventh of the same month… it changed bigness several times, it was sometimes larger than the biggest of those two stars, sometimes smaller than the least of them, and sometimes of a middle size between them. On the twenty-eighth of the same month it was become as large as the star in the beak of the Swan, and it appeared larger from the thirtieth of April to the sixth of May. On the fifteenth it was grown smaller; on the sixteenth it was of a middle size between the two, and from this time it continually diminished till the seventeenth of August, when it was scarce visible to the naked eye.
More stars of the summer sky. Note how Stellarium represents the stars as dots of differing sizes. The web page for Stellarium states that Stellarium “shows a realistic sky… just like what you see with the naked eye….”This system of classifying stars by their apparent sizes dates back to the ancient Greek astronomer Hipparchus, nearly two centuries before Christ. However, following the development of the telescope in the early seventeenth century, astronomers came to realize that the apparent sizes of stars are spurious: Arcturus looks larger than Rho Leo not because of its physical size, but because of its light output and how that light interacts with the eye.
This is perhaps better understood by imagining that one night you and a friend experiment with two identical small LED flashlights, one of which has a weak battery, and the other of which has a very strong battery. Your friend walks two hundred paces directly away from you, then stops, turns on the lights, and aims them both back toward you. The brighter light will appear larger to you than the fainter light, even though both are the same physical size. Try it and see. When it comes to point-like light sources, be they distant flashlights or distant stars, the apparent size you see resides not in the lights but in your eyes.
Thus in the nineteenth century astronomers reworked the magnitude scale so that it wasn’t about size. They came to understand that the light that reaches Earth from a first magnitude star is about 100 times more intense than the light that reaches Earth from a sixth magnitude star. The intensity is measured in power per unit of area—Watts per square centimeter or W/cm2. The magnitude scale is related to light intensity through a factor of 2.5; the light from a (very faint) fifth magnitude star is 2.5 times more intense than the light from a (barely discernable to the eye) sixth magnitude star. A fourth magnitude star (still pretty faint) has 2.5 times the light intensity of that fifth magnitude star and 2.5×2.5=6.25 times the light intensity from the sixth magnitude star. Thus a bright first magnitude star is 2.5×2.5×2.5×2.5×2.5=100* times brighter in terms of intensity than that barely discernable sixth magnitude star.
Why this system? Because the original magnitude scale was based on what the eye sees, and the eye works on a multiplicative scale, not a simple additive one. To see this for yourself, gather up about ten birthday cake candles and turn out all the lights in the room. Look around; it’s dark in the room! Now light one candle. Note how one candle changes things a lot; with one candle you can really see. Now light a second candle, so that two candles are burning. Note how the second candle does make the room brighter, but the change it causes is not as dramatic as the change caused by the first. The third candle causes even less change, the fourth less still, and by the time you go from nine candles to ten you hardly notice the difference. Your eye is not attuned to additive increases in light; each additional candle does not seem to increase the illumination of the room equally, even though each is adding an equal amount of light power. No, your eye is attuned to multiplicative increases in light. Understanding the multiplicative nature of the magnitude scale makes it easier to determine what we are seeing when we look at the stars, and how we know what the stars are.
To know more about the stars, we need to consider what things might affect the intensity of light reaching Earth from a star. These are pretty basic: the distance of the star, and its power output or luminosity. Obviously the farther away a star is, the weaker in intensity its light will be when it reaches Earth and the less bright the star will appear. And obviously a less powerful star will appear less bright than a more powerful star at the same distance.
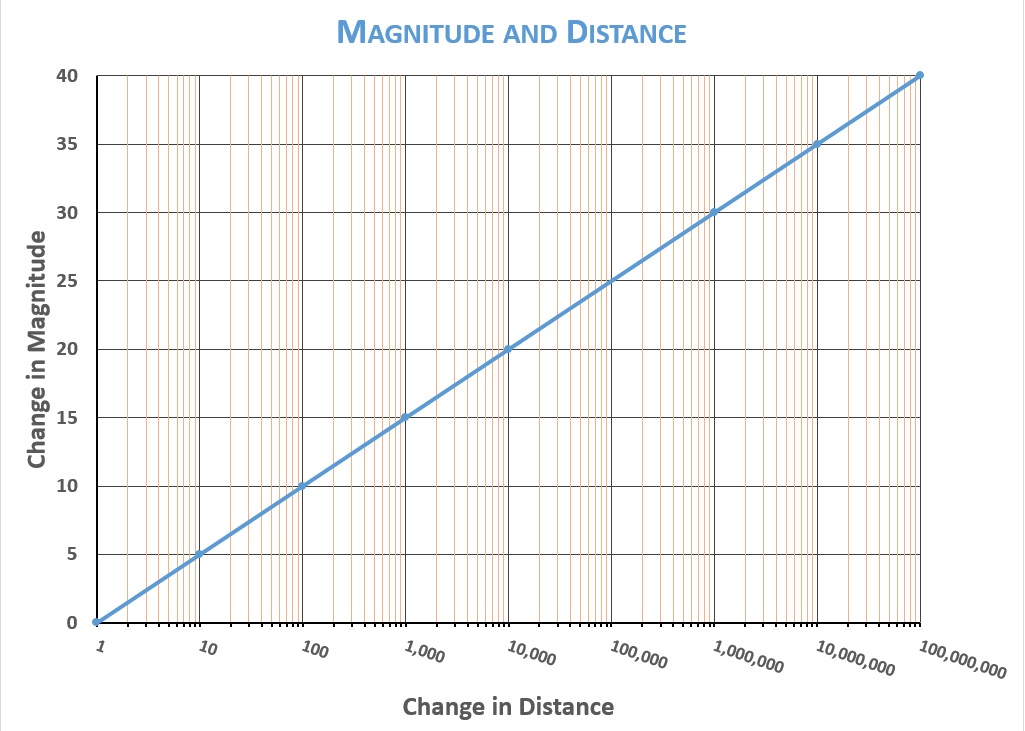
The relationship between distance and brightness is pretty simple. As light travels away from a star, it spreads out in all directions, like an expanding sphere. The surface area of a sphere is determined by the square of the sphere’s radius. Increase the distance to a star by a factor of 2, and you increase the surface area over which the light is spread by a factor of 2×2=4. Thus you decrease the intensity of the star’s light by a factor of 4, too. Increase the distance by a factor of 10, and you increase the area the light is spread over by a factor of 10×10=100, and you decrease the intensity of the star’s light by a factor of 100.
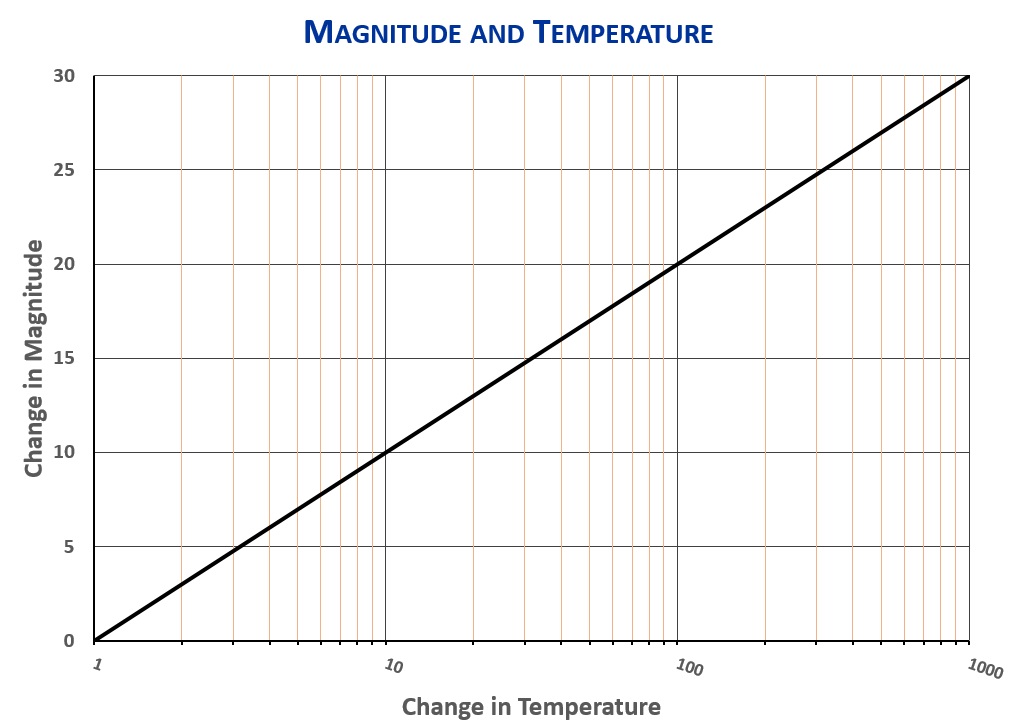
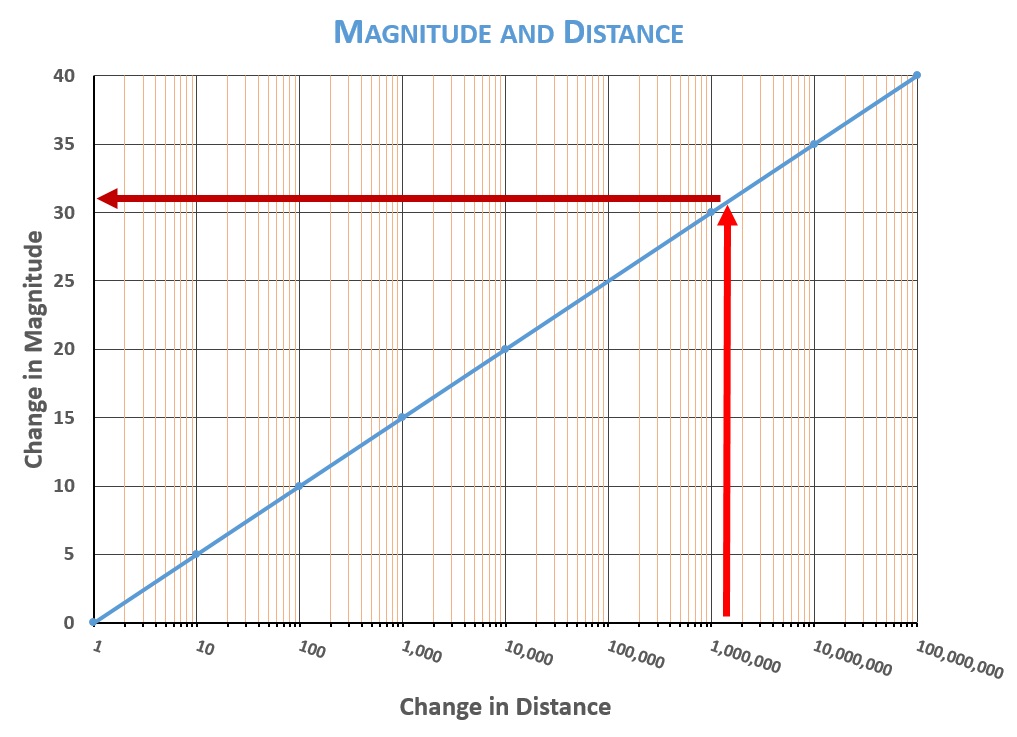
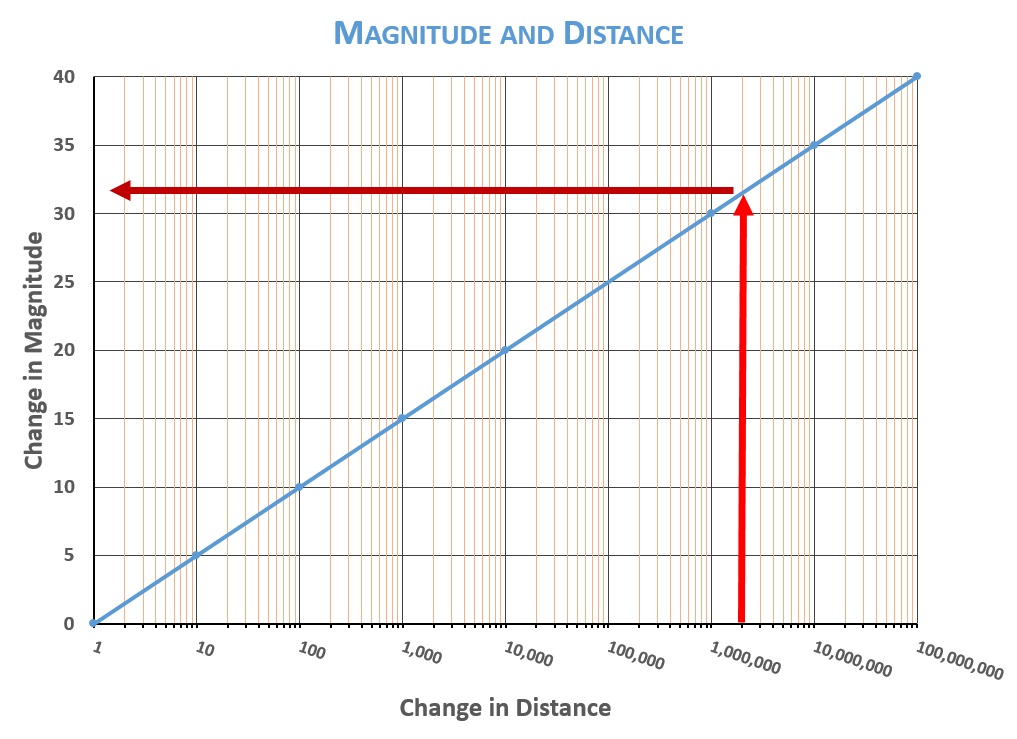
The gray/black sphere is twice the radius of the blue sphere, and has four times the surface area.But a change in intensity by a factor of 100 is a change of five steps on the magnitude scale. The star Spica is a summer sky star whose magnitude is about 1.0. A star identical to Spica but ten times farther away from Earth would be five magnitudes fainter—magnitude 6.0. Were it a hundred times farther from Earth, it would be magnitude 11.0 (too faint for the eye to see, but detectable by telescopes). The graph below shows the relationship between distance and magnitude:
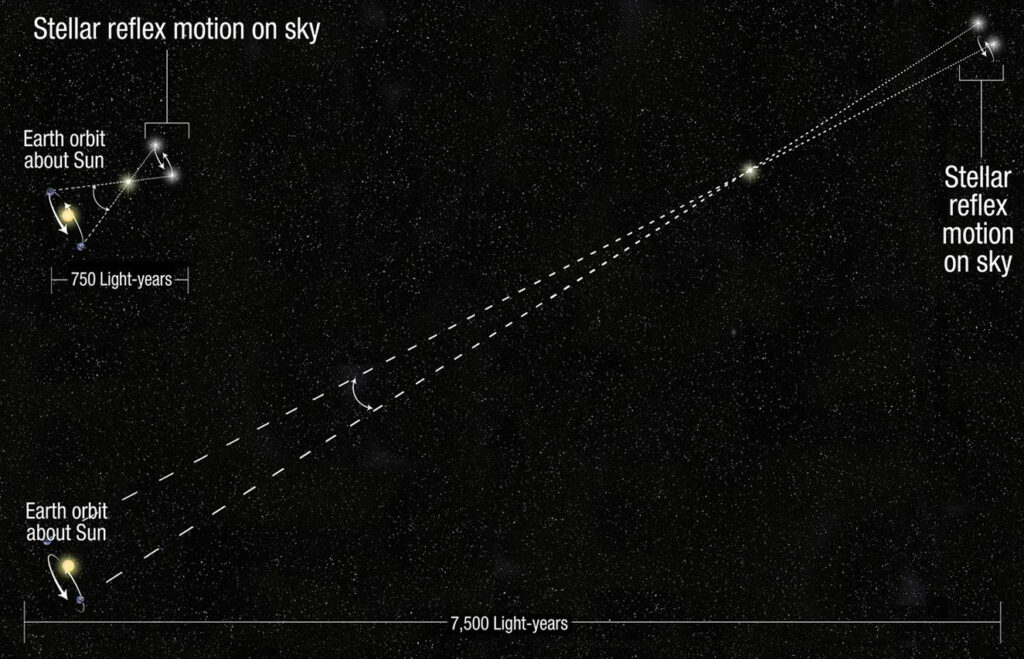
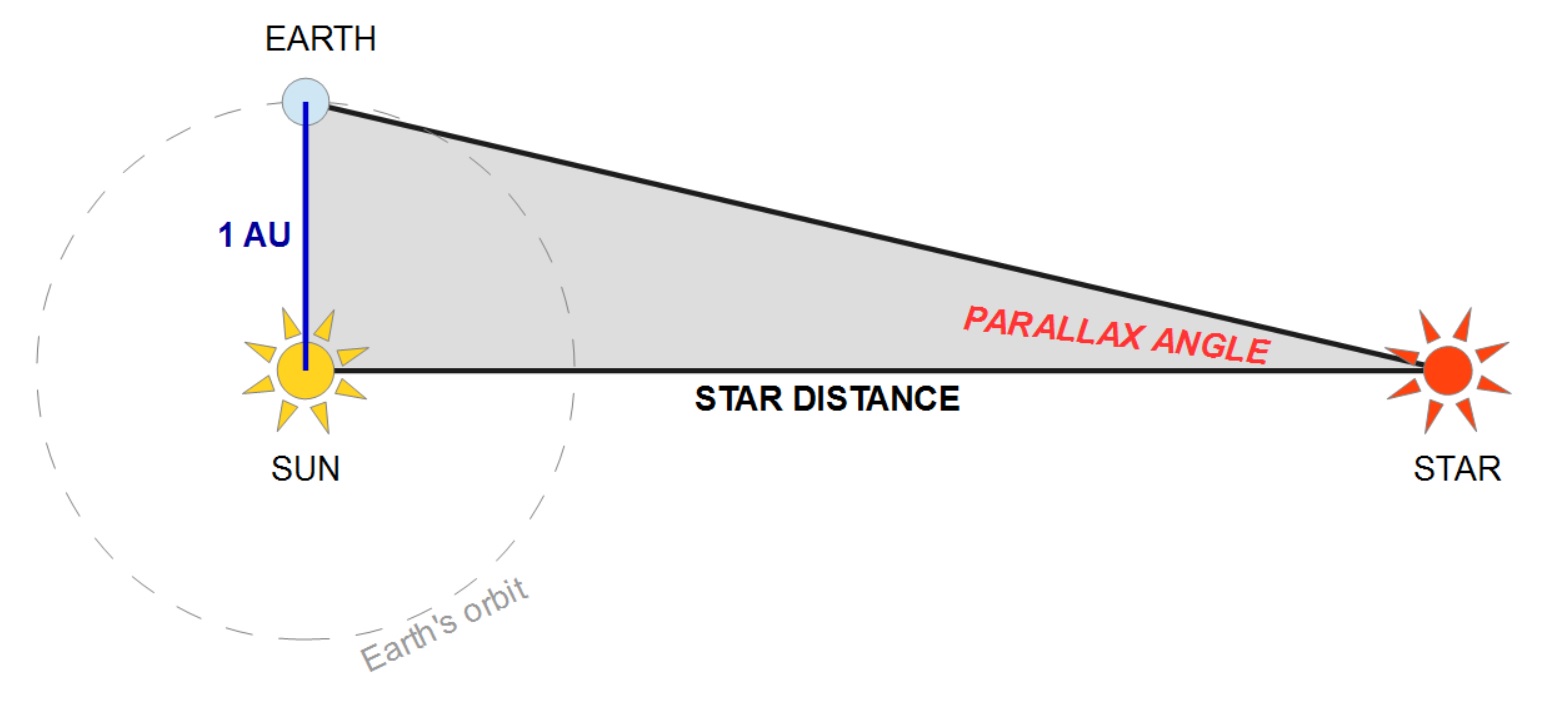
How can we determine the distance to a star? Through the parallax angle created by Earth’s motion about the sun, as illustrated below.
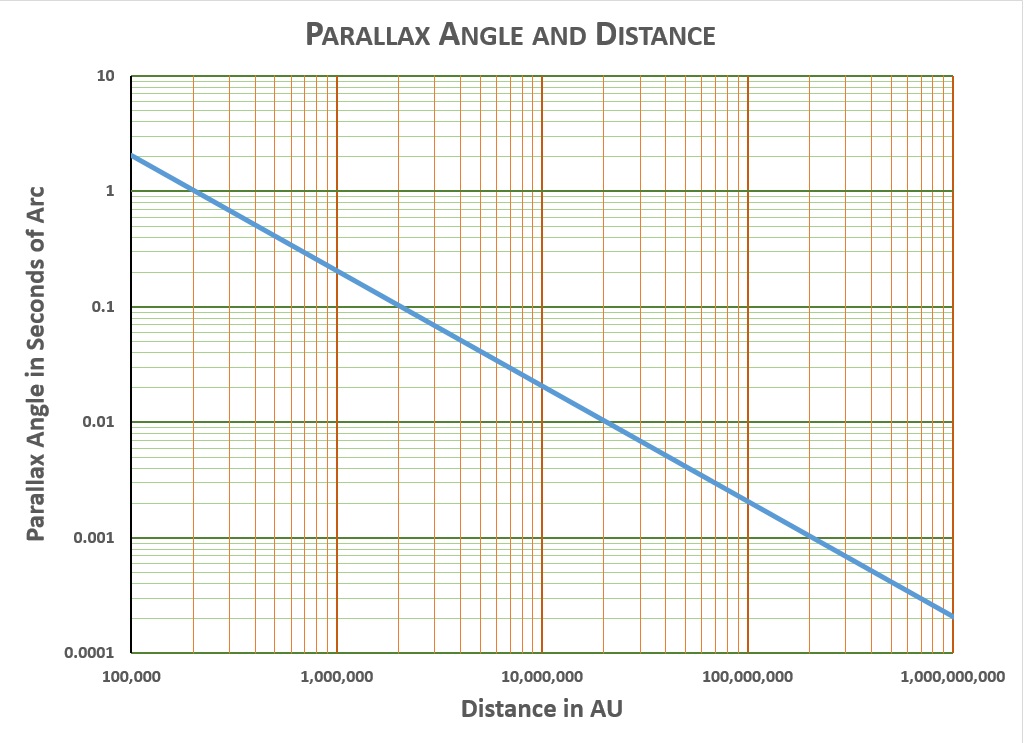
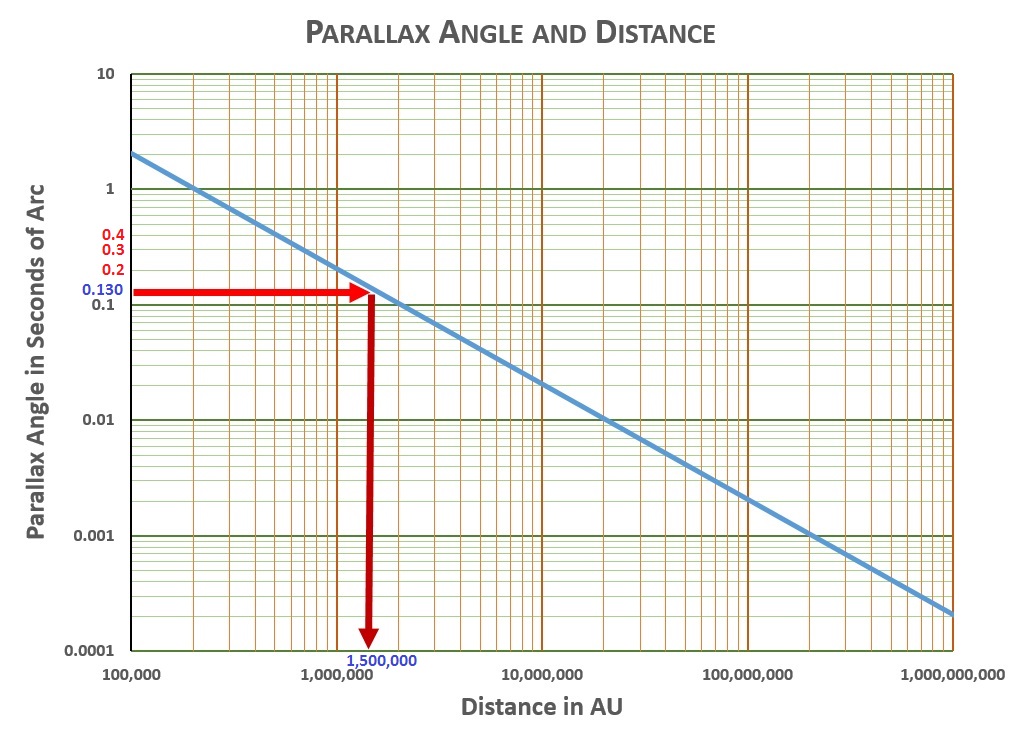
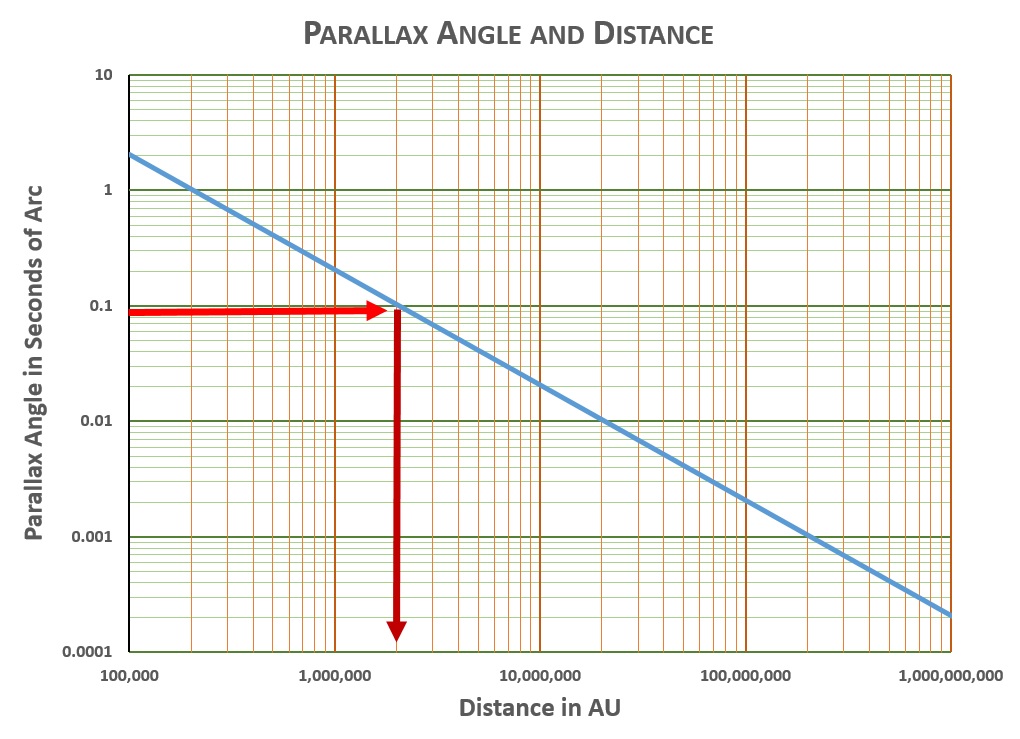
The closer the star, the larger the parallax angle, which is usually measured in seconds of arc (just like there are 3600 seconds of time in an hour—60 seconds per minute times 60 minutes per hour—there are 3600 seconds of arc in a degree). The Earth-to-sun distance is one Astronomical Unit, or AU. This chart shows the relationship between distance in AU and parallax angle in seconds of arc:**
Luminosity is a little more complex of an issue than distance, because luminosity itself depends on a star’s temperature and size. Temperature has the bigger effect. As discussed in a previous post, stars give off light in the same way as, and produce the same continuous ROYGBIV rainbow spectrum as, a piece of glowing hot iron or any piece of glowing hot, dense, incandescent material. So we suppose that the star and the iron have much in common. The proportion of colors in the rainbow emitted by an incandescent body depends upon temperature—the hotter a piece of iron (or a star) is, the more it radiates blue and violet light versus red and orange light. Thus as an incandescent body’s temperature rises its color changes from glowing dull red, to glowing orange-yellow, then white, and then even blue-white. The color of an incandescent body then indicates its temperature. The sun is a yellow star. Stars that are redder in color are cooler than the sun. The coolest, reddest stars are only about half as hot as the sun. On the other hand, the hottest, bluest stars are more than twice as hot as the sun.
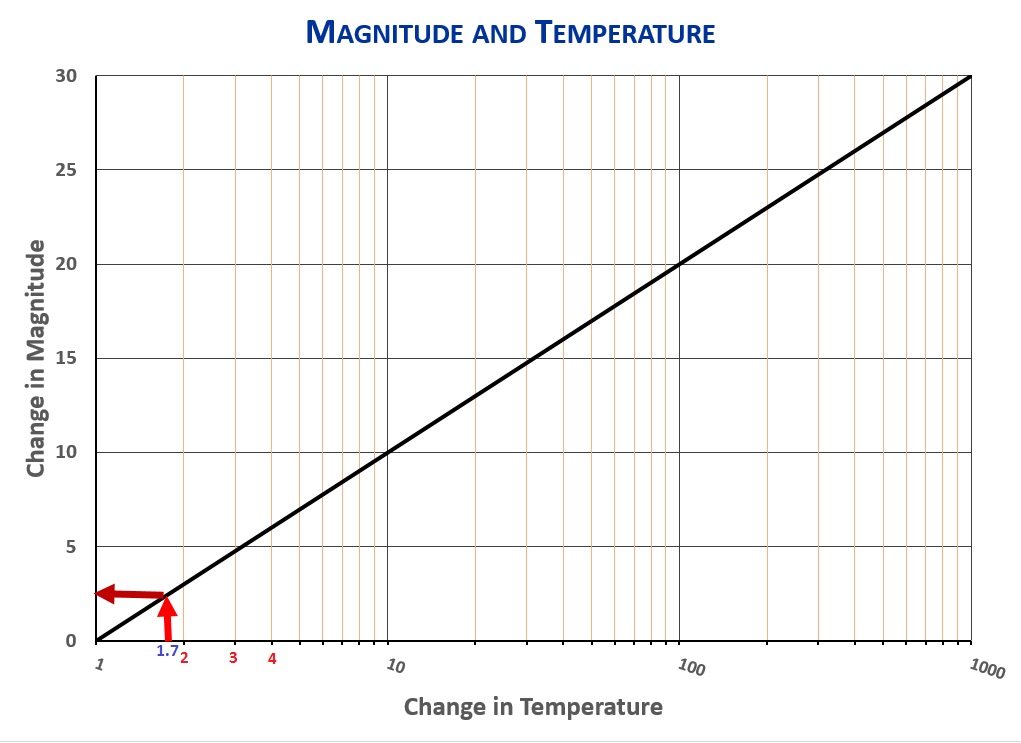
Not only does the color of light emitted by an incandescent body change with temperature, but the quantity of light changes, too. A piece of iron that is glowing orange-yellow is more luminous than if it is only red hot. This effect is tremendous. Luminosity—the “wattage” of light emitted—goes as the fourth power of temperature, meaning that a star that is twice the temperature of Spica (but the same size) will have 2x2x2x2=16 times Spica’s luminosity! A star the same size as Spica but one tenth as hot would be 10x10x10x10=10,000 times less luminous. Since 10,000 is two factors of 100 (100×100=10,000), and since a change of 100 corresponds to five steps on the magnitude scale, a star one tenth as hot as Spica would be 10 steps down on the magnitude scale, at magnitude 11.0. The relationship between temperature and magnitude is shown here:
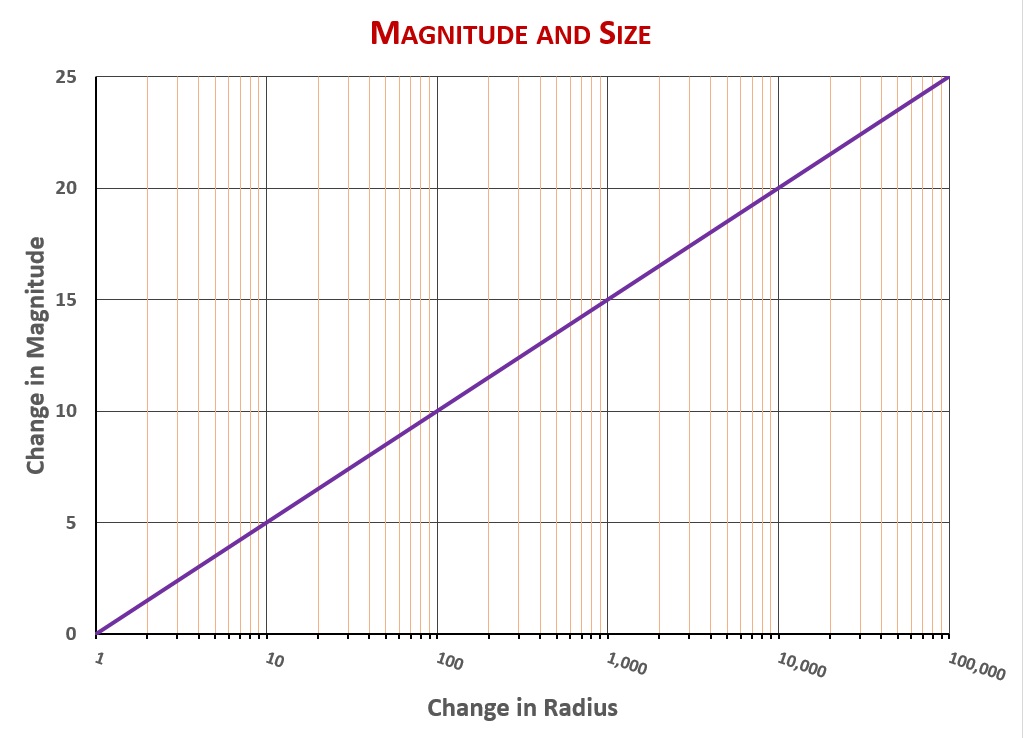
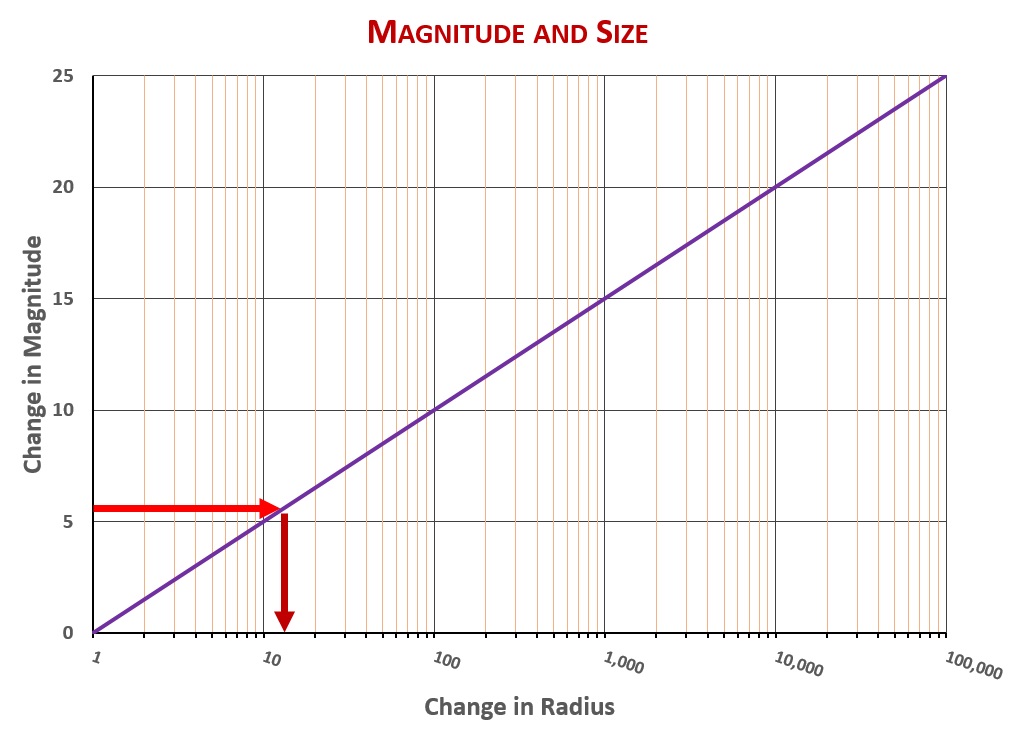
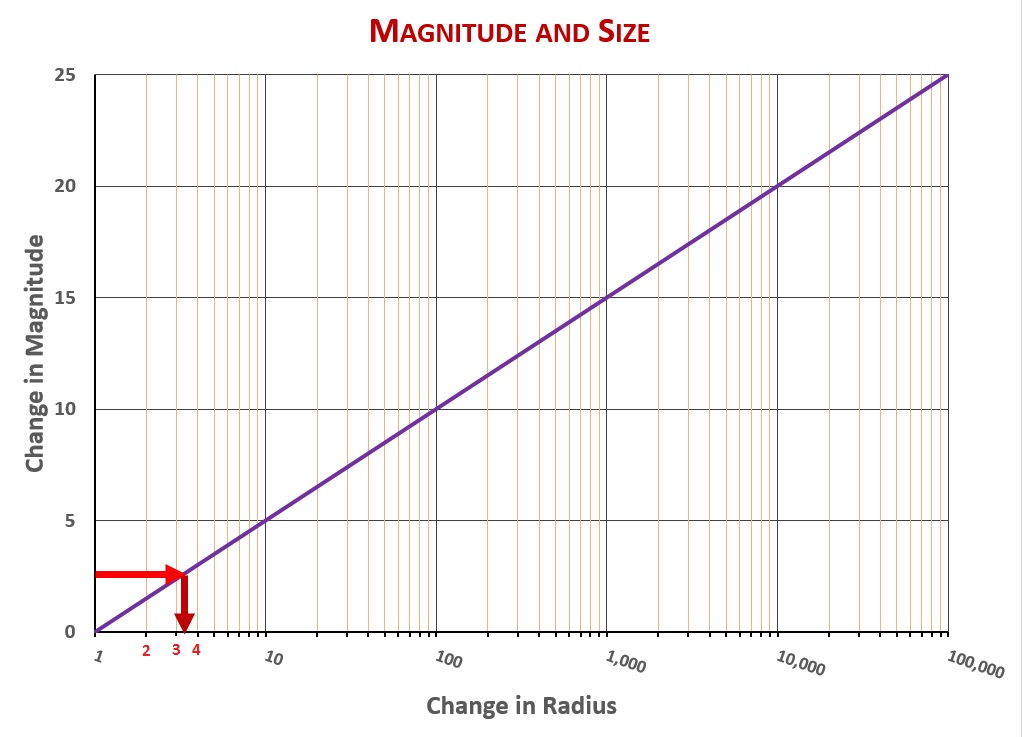
Size has a lesser effect on luminosity than temperature. Luminosity follows the surface area of a star, and since surface area of a sphere goes as the square of radius, a star twice the radius of Spica (but the same temperature) would have 2×2=4 times the luminosity. A star one tenth the radius of Spica (but the same temperature and the same distance from Earth), would be 10×10=100 times less luminous—and thus five steps down from Spica on the magnitude scale, at magnitude 6.0. Here is a graph of the relationship between size and magnitude:
We now have everything we need to figure out what these stars we see really are. Let’s begin with Vega. Vega is magnitude 0.0—one step brighter on the magnitude scale than the summer star Spica, which is magnitude 1.0. Vega’s parallax is 0.130 arc seconds. Reading off the parallax chart, we find a parallax of 0.130 arc seconds corresponds to the star being 1,500,000 AU distant (1,500,000 times more distant than the sun).
So suppose Vega were in the place of the sun—that is, suppose somehow we could magically replace the sun with Vega, which would make Vega 1,500,000 times closer than it currently is. According to the magnitude and distance chart, making Vega 1,500,000 times closer would make it about 31 steps of magnitude brighter.
Vega is 0.0, and smaller numbers on the magnitude scale mean brighter (a 1 is brighter than a 5, a 0 is brighter than a 1, a minus 1 is brighter than a 0, a minus 5 is brighter than a minus 1, etc.), so making Vega 1,500,000 times closer would make it a minus 31. The sun, by contrast, is minus 27. So, were Vega in the place of the sun it would be four magnitude steps brighter than the sun. Four magnitude steps means 2.5×2.5×2.5×2.5=39 times the sun’s luminosity. Vega seems to be much more powerful than the sun.
That makes sense. Vega is bluer than the sun, and therefore hotter. In fact, based on its color, Vega should be about 1.7 times hotter than the sun. Judging from the magnitude and temperature chart, being 1.7x hotter would only make Vega about 2 magnitudes brighter than the sun at the same distance.
So Vega must also be larger than the sun. According to the magnitude and size chart, to account for the remaining 2 magnitudes of brightness, Vega must be about 3.3 times the sun’s radius.
Let’s try Arcturus. It has magnitude 0.2, with parallax 0.089 arc-seconds. From the parallax chart we get that Arcturus is about 2,000,000 times the sun’s distance.
If we put Arcturus where the sun is, we make it 2,000,000x closer. According to the charts, that will make Arcturus about 32 steps brighter on the magnitude scale. Were Arcturus where the sun is, it would be magnitude negative 31.8—we’ll just say minus 32. That is five steps of magnitude brighter than the sun at the same distance. That makes Arcturus 100x more luminous than the sun.
But Arcturus is a golden yellow star. It is a little redder, and thus a little cooler, than the sun. Its color tells us that it is about 9/10 the sun’s temperature, so the sun is 10/9 its temperature. Were Arcturus the size of the sun, the sun would be the more luminous, but only by a magnitude or less according to the charts.
Therefore the reason Arcturus would be five magnitudes brighter than the sun were it at the same distance as the sun has to be because Arcturus is larger than the sun. According to the size and magnitude chart, that five magnitude (plus the half or so magnitude due to temperature) difference means Arcturus must be about 14 times the sun’s radius.
So, we have reasoned out that Vega must be about 39x more luminous than the sun, and 3.3x larger (in terms of radius). We have reasoned out that Arcturus must be about 100x more luminous than the sun, and 14x larger. Let’s “check” our answers using the Celestia computer app. Celestia gives the luminosity of stars and can show us what different stars would look like were they in the place of the sun.
According to Celestia, Vega is 49.1x as luminous as the sun, and about 3x as large, while Arcturus is 113x as luminous and 25x as large. So our calculations are in general agreement with Celestia. That’s not too bad, since Celestia’s values are no doubt based the work of astronomers who used more sophisticated and precise reasoning and measurements than these limited charts!
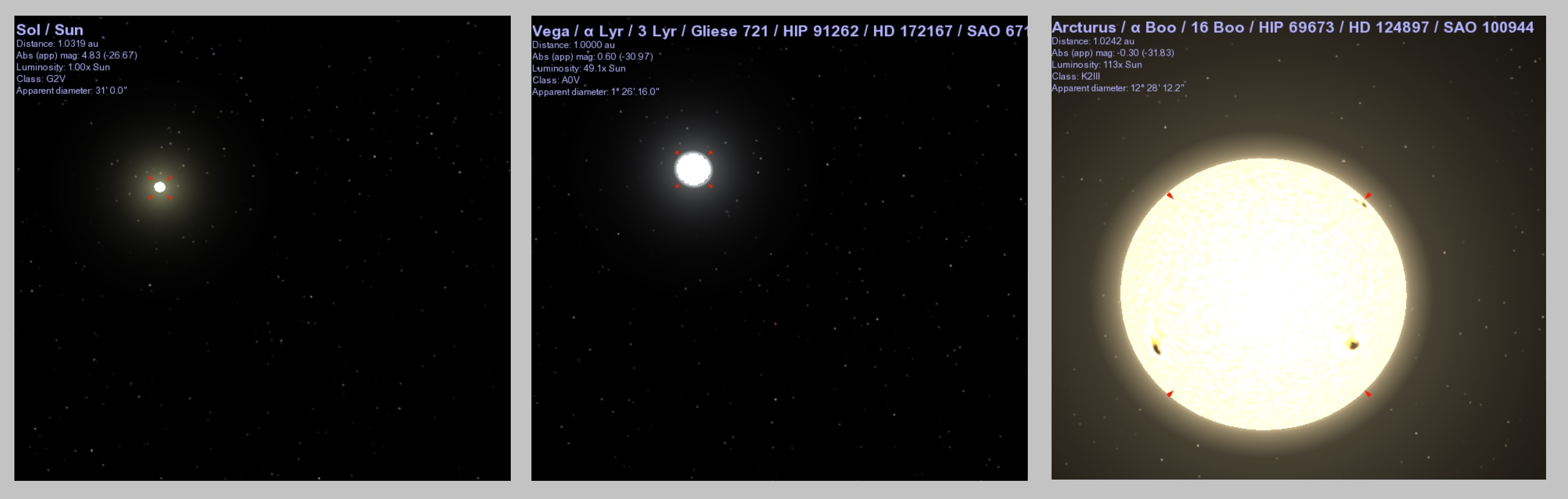The sun, Vega, and Arcturus as they would appear from a distance of 1 AU (the distance of the Earth from the sun), according to the Celestia app.There are stars more powerful than Arcturus. Consider Antares, in the constellation of Scorpius.
More stars of the summer sky as represented by the Stellarium planetarium app, including the stars of Scorpius. Antares is at center, slightly toward the top.According to Celestia, Antares is over 9000x as luminous as the sun, even though it is only about half as hot. The luminosity of Antares is owed to it being so huge that, were it in the place of the sun, the Earth would be deep inside it! Antares is bigger than Earth’s orbit.
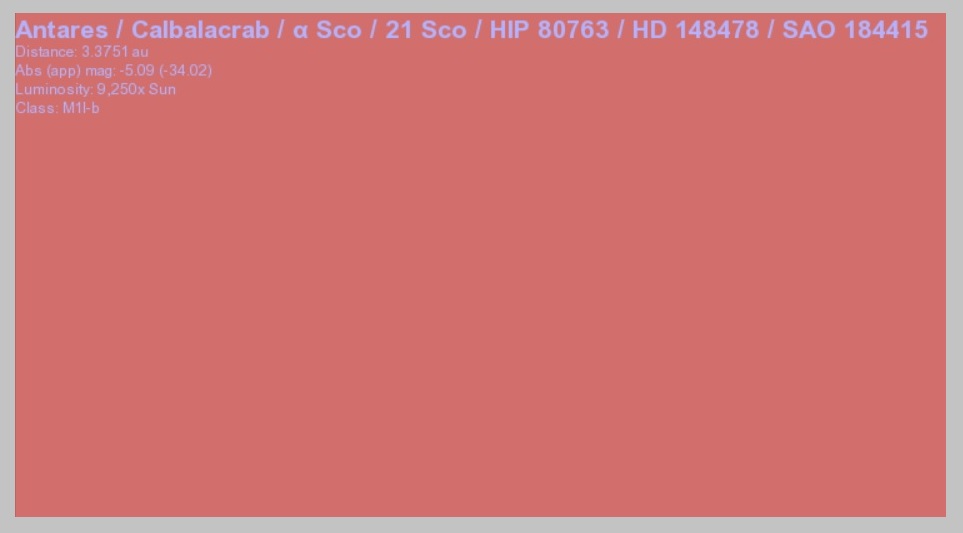Antares is so huge that, were it in the place of the sun, Earth would be inside the enormous red star.Then there is Rho Leo, which doesn’t look like much in the sky, but that is only because it is so far away. Celestia says Rho Leo is almost 70,000x more luminous than the sun.
Rho Leo (circled).
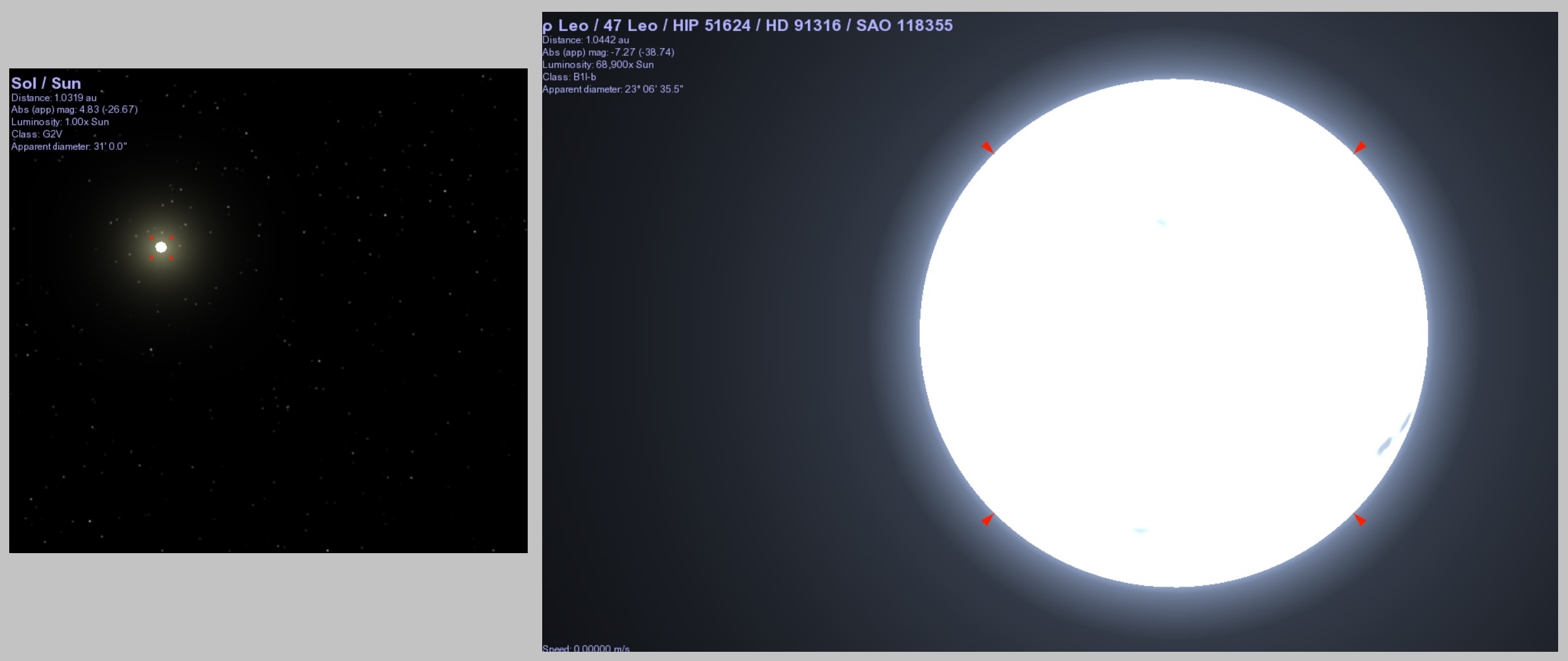The sun and Rho Leo as they would appear from a distance of 1 AU, according to the Celestia app. However, Celestia cannot represent the blinding brilliance of Rho Leo’s surface.Don’t be surprised that so many of the stars visible in the summer sky are more powerful than the sun—luminous stars stand out. There are plenty of sun-like stars out there; they just do not stand out. Consider HIP 80337, a dim star in Scorpius.
HIP 80337 (circled).According to Celestia, HIP 80337 is very sun-like: same size, same color, same luminosity. Put HIP 80337 in the place of the sun and it would look pretty much the same.
HIP 80337 has about the same parallax as Arcturus, and therefore is about the same distance. When you look at HIP 80337 you are seeing what the sun would look like if it were where Arcturus is.
Now consider Barnard’s Star. It is a summer star, but you cannot see it without a telescope, even though it is not half as distant as even Vega.
The location of Barnard’s star.Like Antares, it is not very hot, but unlike Antares, it is small. According to Celestia, it is not even one half of one thousandth of the sun’s luminosity. Or consider the star 2MASS J18353790+3259545, near Vega. Celestia says its luminosity is just a tiny fraction of Barnard’s star! Were 2MASS J18353790+3259545 to be put in the place of the sun, it would look so small as to be almost star-like. It would glow red like a piece of charcoal, and provide less light than a full moon. Astronomers believe that small, dim, red stars like Barnard’s and 2MASS J18353790+3259545 comprise the vast majority of stars in the universe—we just can’t see them.
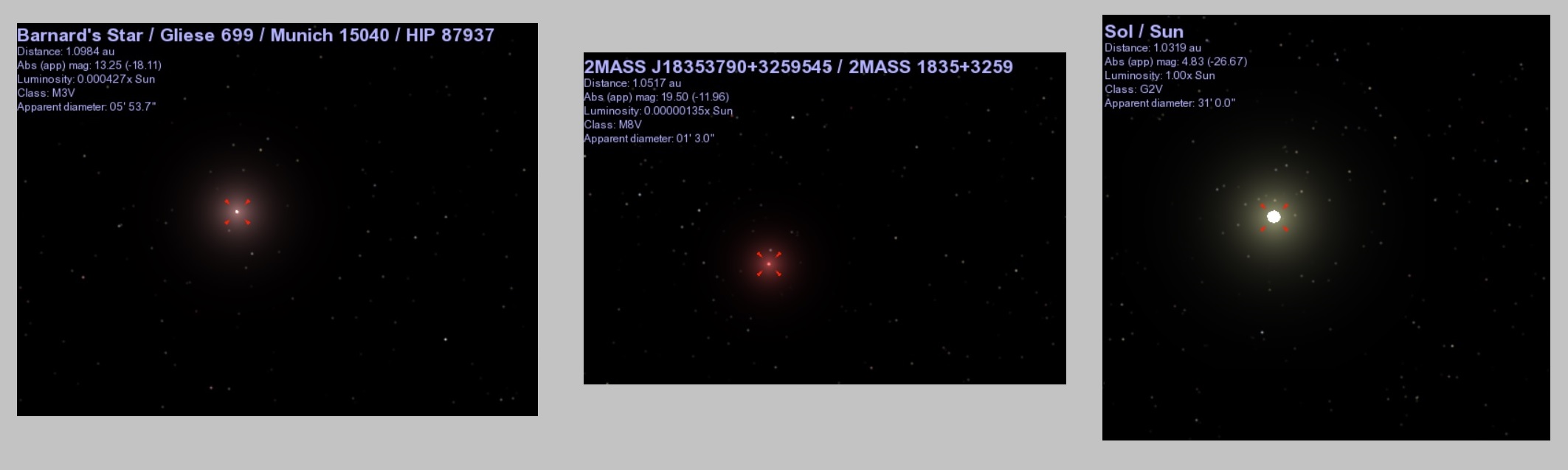Barnard’s Star, 2MASS J18353790+3259545, and the sun as they would appear from a distance of 1 AU, according to the Celestia app.So now we know what some of the summer stars are. More importantly, we know how we know what the summer stars are. We see that the sun is definitely a star: HIP 80337 is a star, and the sun and HIP 80337 are pretty similar. But are the stars suns? Antares is giant compared to the sun; Rho Leo is blinding compared to the sun; 2MASS J18353790+3259545 is puny compared to sun. And the differences between these stars and the sun pale compared to the differences among themselves—consider 2MASS J18353790+3259545 versus Antares or Rho Leo. Perhaps the safest thing to say is that there is an incredible amount of diversity among the summer stars.
We have learned how we know what the stars are, and using that knowledge we have seen that while the sun is certainly a star, the summer stars themselves vary wildly in size and in power or luminosity. Among such incredible stellar diversity are many bodies that are very different from the sun. But all this knowledge about the stars came from just three measurements: (1) An annual motion of a star (parallax), (2) The magnitude of that star, (3) The color of that star.
We do not measure the size of a star like we might measure the size of a window with a ruler. We do not measure the distance to a star like we might measure the distance to a friend’s house with our car’s odometer. We do not measure the power output of a star like an engineer might measure the output of a new kind of light bulb. We have never been to a star to make such direct measurements, and we are not likely to go to one in the near future. Rather, we measure movement, magnitude, and color, and from these things we reason mathematically to determine the star’s size, distance, temperature, and luminosity. We reason by analogy—the light of stars matches the light given off by a dense, incandescent object like a piece of hot iron. We suppose that stars and incandescent iron behave in the same basic ways: the luminosity of an iron ball increases as the square of its radius and the fourth power of its temperature, thus so does the luminosity of a star. In short, we suppose that the heavens and the Earth are under the same rule.
If we are wrong about the specific supposition that stars and glowing iron have something in common, we may be very wrong about the sizes and luminosities of stars now, but we can hope to figure things out better in the future. And we can imagine why there might be limits to this sort of supposition. For example, my fellow blogger Brenda Frye has noted that there is a limit to how massive a star can be, and that limit is only about 150 times the mass of the sun. But Antares takes up much, much more than 150 times the volume of the sun. Antares must be a lot less dense than the sun. How much less dense can Antares be before it stops being a “dense, incandescent body,” and the analogy to iron breaks down, throwing off our mathematical reasoning? On the other hand, if we are wrong about the general supposition that the heavens and the Earth are under the same rule, so that in fact maybe the stars are controlled by magic Elves who choose the coloring and brightness and motion of the stars for their own inscrutable Elvish reasons, that would do more than throw off our reasoning a bit. That would mean that we could never hope to know anything about the stars other than their motion, their magnitude, and their color. That would really stink.
Keep this in mind when you look up at the summer stars, or when you hear about how far away a certain star is, or how large or powerful it might be. It is cool, cool, cool to be able to look up at the summer sky and see the stars, and know something about what you are looking at, and to know how you know what you know, and to know why it is even possible to know what you know. There is so much to see and think about in the stars of the summer sky.
*OK, for those of you who multiplied this out and found out that the result is not 100 but 97.66… well, actually the multiplying factor in the magnitude scale is not exactly 2.5, but 2.5118864…. This number is called “Pogson’s ratio,” after N. R. Pogson, the British astronomer who proposed this system in 1856.
**For those who want the math of the parallax-and-distance chart: For the small angles involved in parallax the relationship between parallax and distance is simple:
PARALLAX ANGLE = EARTH-to-SUN DISTANCE / STAR DISTANCE
In terms of AU, this is
PARALLAX ANGLE = 1 AU / STAR DISTANCE IN AU
This formula gives the parallax angle in radian units. There are 57.3 degrees in a radian, and 3600 seconds of arc in a degree, so to get this formula to work in seconds of arc it needs to have those correction factors built in
PARALLAX ANGLE = (1 AU / STAR DISTANCE IN AU) x 3600 x 57.3
This last formula is what is plotted on the chart.
