One evening last month my wife and I were watching a lovely sun set and were struck by the changing illumination of the clouds after the sun had disappeared below the horizon. First, sunlight shone up on the undersides of the clouds. Then, gradually, the lower clouds grew dark while the higher clouds remained lit. Finally, even the high clouds went dark.
And this of course led me to the obvious question:
Where is the edge of the Earth?
After all, those clouds were darkened by the Earth’s shadow passing over them. See the figure below. The flat Earth is in dark green. When the sun is at some angle A below the horizon of a flat Earth, a higher cloud (1) will be lit (from below) by the sun’s rays while a lower cloud (2) will be in the shadow and dark. If we know the height H of cloud 1 and the angle A, we can calculate the distance D from the spot under the clouds to the edge of the Earth.
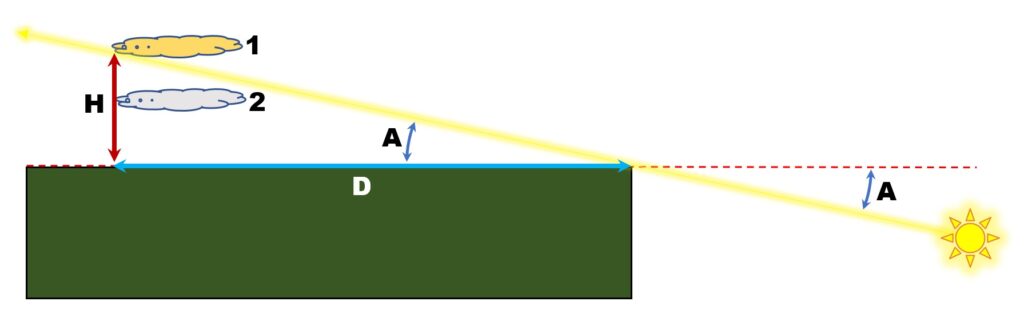
How would we determine A? As the rises, sets, and rises again, it completes a circuit of 360 degrees in 24 hours of time. That is 15 degrees per hour; 0.25 degrees per minute. Knowing the time of sunset, the direction the sun is moving at sunset, etc., we can use the 0.25 deg/min value to determine just how far below the horizon the sun will be at any moment after sunset.
What about the cloud height H? Airliners flying at 30,000 feet or so fly well above most clouds. We could reasonably estimate H as 20,000 feet.
Let us then determine the distance to the edge of the Earth. Refer to the photograph below. It shows a cloud above Louisville, Kentucky, illuminated by the sun while clouds below it are dark. It was taken at 8:54:42 PM on May 23 of this year (thank you, camera, for stamping that information on the image file). At that moment the angle of the sun below the horizon was A = 0.8729 degrees.*
Calculating the distance D is an exercise from high school trigonometry: the tangent function for triangles. If H = 20,000 ft and A = 0.8729 deg, trigonometry says D = 1,312,600 ft, which is approximately 250 miles.*
Thus, if the Earth is flat, the edge of the world is just 250 miles away! Denver, Las Vegas, and San Francisco all must not exist. Nothing must exist west of the Mississippi River. The Vatican Advanced Technology Telescope (VATT), located on Mt. Graham in Arizona, must not exist, either. If the Earth is flat.
Alter the height of the clouds a bit and things do not really change: Were the illuminated clouds in the photo at 40,000 ft then the edge of the world would be 500 miles away. There would still be no Denver, no VATT, etc. If the Earth is flat.
Of course, the point here is that obviously the Earth is not flat! Watching a sunset shows that the Earth does not even look flat. We can see from the light on the clouds that the edge of a flat Earth would be too close (the light is not a problem for a globe Earth).
I love carping on the shape of the Earth. It is such a great illustration of the basics of science, and of the problems our modern society has with science. Modern flat-Earth-ism is something all my recent students have been familiar with; some of them even claim to think themselves that the Earth is indeed flat. Flat-Earth-ism is a creature of the internet, but it is also a creature of our modern approach to knowledge itself, of our modern insistence that knowledge consists of believing what experts tell us (especially those experts whose proclamations mesh with our own world views; especially when the topic involves math). That modern insistence means that too often we teach children in school that the Earth is round, but do not teach them how we know that it is. So they end up finding flat-Earth-ism plausible, because to them the fact that Earth is round is just something some expert says.
But science is not based on what experts say. It is based on observing and measuring the real world, thinking critically and mathematically, and seeing for ourselves: “reproducibility” is the word. We can’t personally reproduce every scientific result, of course—to a great extent we must rely on other scientists, and especially on past scientists, who became the experts by doing the observing, measuring, and so forth.
But it is good to personally reproduce and verify some things. Sometimes we can do that just by watching a sun set and seeing the light play upon the clouds.
*While calculating A is not hard, I found its value of 0.8729 deg the really easy way: I plugged in the date and time into the Stellarium planetarium app and it gave me the angle, which agreed with my rough analysis. To find D, I used
tan(A) = H/D
so
D = H/tan(A) = 20,000 ft/tan(0.8729) = 1,312,600 ft.
Lastly,
1,312,600 ft / 5280 ft/mile = 248.6 miles.
