St. Augustine famously said that God exists outside of time: time is a creation of God, along with the universe; thus there was no “before” the moment of creation. Modern physics tells us something similar. The Big Bang theory, developed by the Belgian physicist Fr. Georges Lemaître who built upon the ideas of Albert Einstein, says the universe emerged from a state in which space and time were distorted beyond what the laws of physics allow us to investigate. Time began with the Big Bang. Lemaître described the universe as beginning on a “day without yesterday”.
How can space and time be distorted? I have discussed this some in my series of posts on Black Holes. Now we dig into the topic more in this new series of posts (click here for all three posts in the series).
PART 2
In Part 1 we looked at Einstein’s idea that the speed of light is the same, a constant, for all observers. If you accept this “constant” idea, things get strange, including time and space. And you don’t have to be an Einstein to see this.
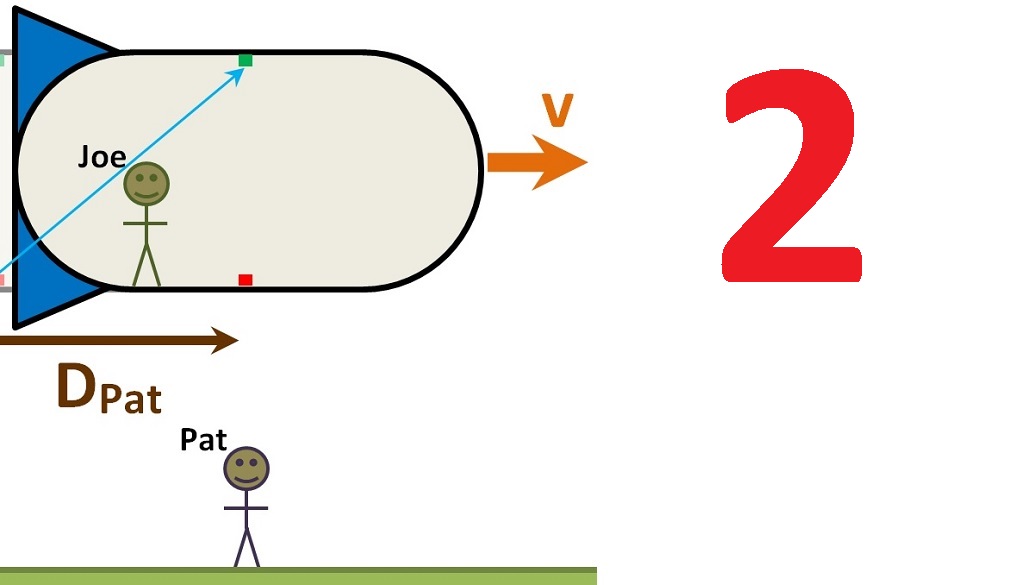
For example, suppose Joe has a space ship (below). In the ship, Joe has a light emitter (the red box) on the floor of the cabin of the ship, and a light detector (the green box), on the ceiling.
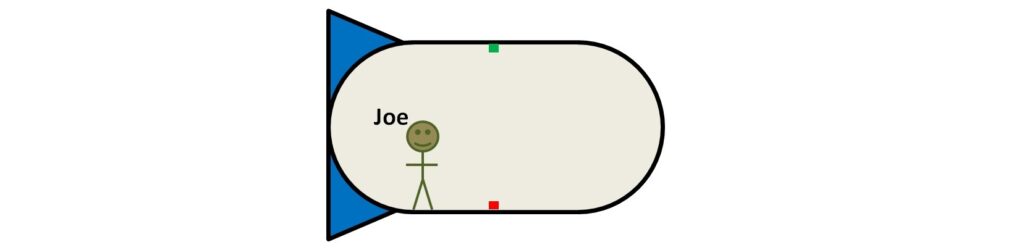
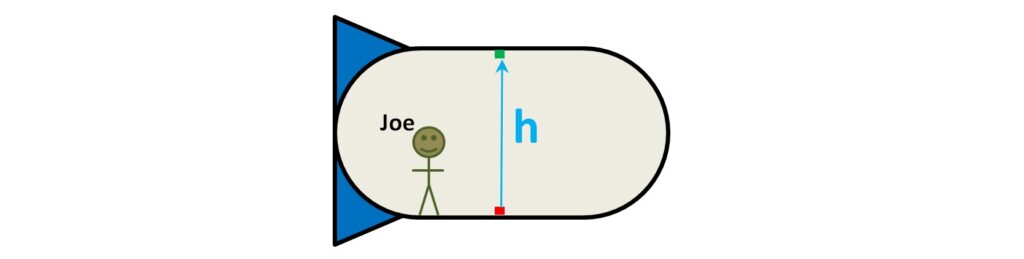
Joe triggers the emitter to send out a pulse of light, which travels the height of the cabin (h) and hits the detector. The time it takes for the light to travel this distance is time = distance/speed (if you drive 200 miles at an average speed of 50 mph the trip will take 200/50 = 4 hours). This process is not altered by any steady motion of the ship, as you know well if you have ever travelled on a smooth-moving plane or ship or train (you can’t really tell it is moving, unless you look out a window, in which case you just see the outside world moving past you).
Now let’s bring in an outside observer, Pat. Pat sees Joe’s ship moving to the right at steady speed V. Pat will see the following as Joe sets off the light pulse:
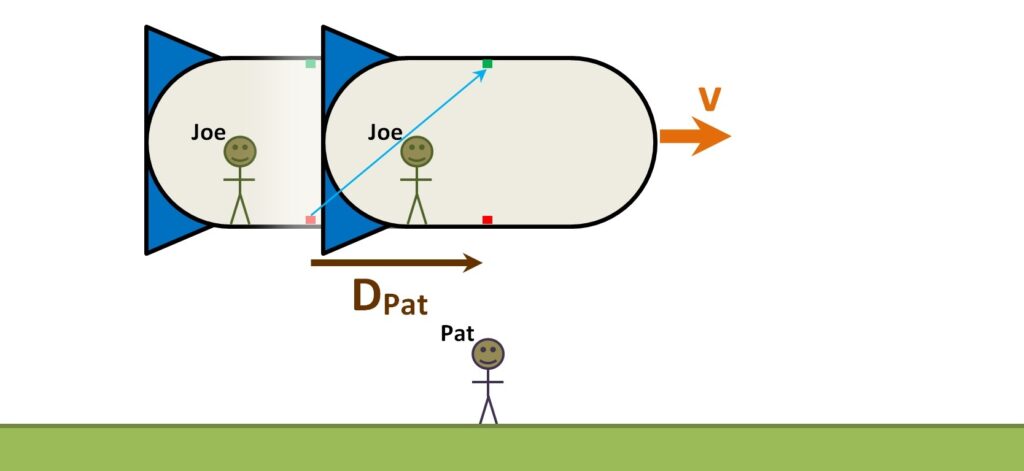
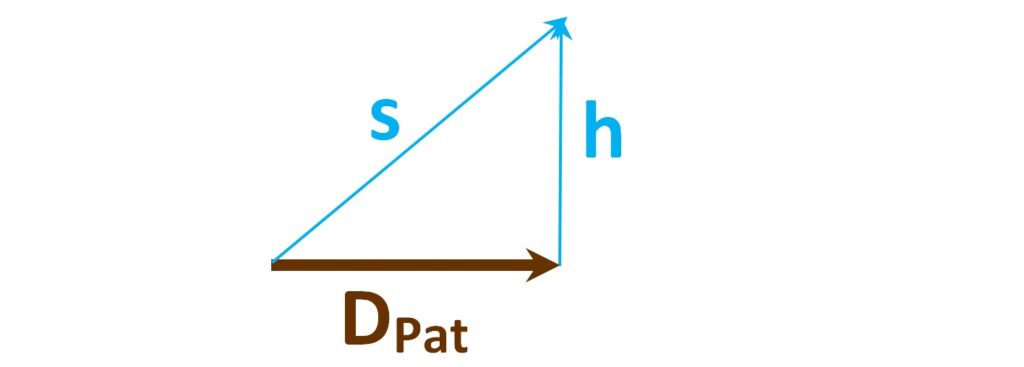
While the pulse is travelling the height of Joe’s ship, Pat sees the ship move to the right by the distance DPat. Since the light leaves the emitter at one end of DPat and strikes the detector at the other end, Pat sees the light pulse travel the length s of the hypotenuse of the right triangle formed by DPat and h. That length is longer than just the vertical distance h.
If the pulse was not light, but sound, then Pat would see it move faster than Joe would. That is because Pat would see the air in Joe’s cabin (the medium for the sound pulse) moving to the right. The speed Pat measured for the sound would be the combination of the ship’s speed plus the sound speed, much like the truck and ball in Part 1 of this series.
But the pulse is light, not sound. And, according to Einstein, there is no medium for light; light travels at speed c for all observers. Pat sees the pulse move at c just like Joe does. Therefore the time Pat measures for the light to go from emitter to detector is the hypotenuse length divided by c. Because the hypotenuse is longer than h, the time Pat measures is longer than the time Joe measures. It is longer by a factor called γ:
tPat = γ × tJoe
The factor γ will depend on the ship’s speed; the slower the ship, the shorter DPat is and the shorter the hypotenuse.* Let’s suppose the ship is moving at such a speed that the hypotenuse is twice the length of h. This means γ = 2 (which requires V to be 86.6% the speed of light*). Pat sees the light take twice as long to travel from emitter to detector as Joe does.
Yet that trip of the light pulse corresponds to a certain time interval on the ship — a certain fraction of seconds, a certain fraction of a beat of Joe’s heart, a certain amount of aging of Joe’s body, a certain amount of growth in Joe’s on-board house plant. Pat sees everything on board the ship taking twice as long as Joe sees it. To Pat, everything on the ship is moving at half-speed, including Joe’s heartbeat and the plant’s growth. Pat sees time slowed down for Joe. If Joe keeps travelling at 86.6% c for one year as recorded by the ship’s clock, Pat’s clock will record two years passing. Thus Pat will say “I am aging more rapidly than Joe!” Time runs at different rates for Pat and Joe. This is what is known as time dilation.
Of course, Joe sees Pat moving past at speed V, too, and claims just the opposite! But for the two to get together and compare ages and clocks and house plants requires their relative motions to stop, and that means the situation is no longer one of steady speeds, and all this stuff gets a lot more complicated.
Because the time measured by two different people is dependent on their relative velocities, distance measurements are also affected, also by an amount of γ. This effect is known as length contraction.
The time that an event takes as measured in a frame of reference at rest with respect to that event is called the proper time. Continuing with our idea that Joe’s ship is moving such that γ = 2, let us now suppose that Joe needs to “answer the call of nature”, and spends 5 minutes in the ship’s bathroom as measured by a clock on board ship. The proper time for the bathroom visit is 5 minutes. As observed by Pat, that visit took 10 minutes.
Suppose further that at the moment Joe steps into the bathroom, the ship passes a marker (A). At the moment Joe steps out of the bathroom, it passes a second marker (B). The length between A & B as measured by Pat, who is at rest with respect to those marks, is called the proper length, Lproper.
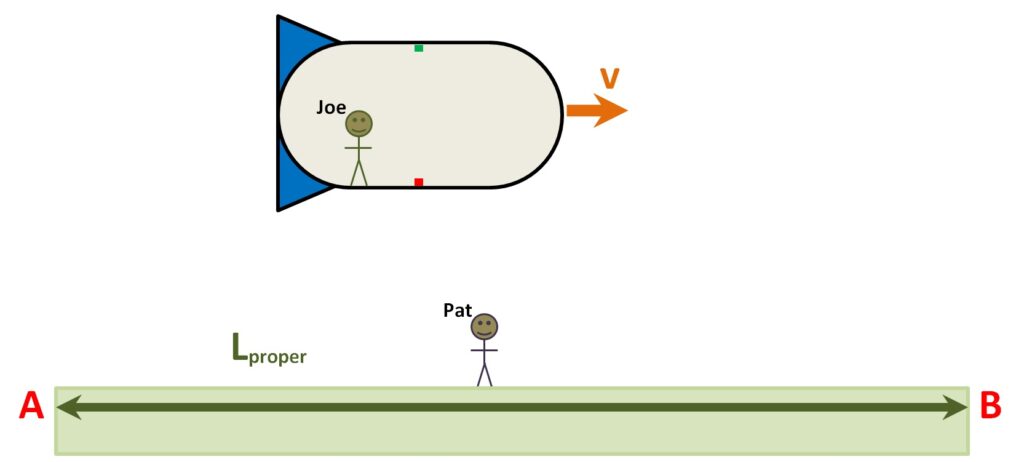
Pat can use the speed of the ship to determine that length: Lproper = V x 10 minutes. However, from Joe’s point of view, A, B, and Pat are all moving past at speed V. Furthermore, the time between A & B for Joe was 5 minutes. Therefore, Joe measures the distance between A & B to be V x 5 minutes; that’s half what Pat measured. Joe sees the distance from A to B as being shortened. This is the length contraction effect. Length is shortened by the amount of γ.
Thus time and length, that is, time and space, can be distorted. These effects are observed to happen. We cannot build ships that go 86.6% the speed of light, but we can accelerate small particles, like unstable (radioactive) atoms to such speeds. If we launch them down some long tube at V = 86.6% c, time is reduced by half for them, so the number that disintegrate on the journey through the tube is reduced by half of what we would expect if we did not know about Einstein’s ideas. Lots of experiments have confirmed that Einstein was right about the constant nature of the speed of light, and about the distortability of space and time that is a consequence of that luminous constancy.
But wait! There’s more! In the next post in this series, we’ll talk about some even stranger distortions of time.
*For the mathematically inclined:
γ can be derived by the Pythagorean Theorem. Consider the right triangle formed by DPat and h:

DPat depends on the ship’s speed V and the time Pat measures (tPat) for the light to travel from emitter to detector: DPat = V tPat.
h is the speed of light multiplied by the time Joe measures (tJoe) for the light to travel from emitter to detector: h = c tJoe.
The hypotenuse length s depends on the speed of light and the time Pat measures for the light to travel from emitter to detector: s = c tPat.
But s can also be found from the Pythagorean Theorem:
s2 = DPat2 + h2
So, substituting:
(c tPat)2 = (V tPat)2 + (c tJoe)2
c2 tPat2 = V2 tPat2 + c2 tJoe2
c2 tPat2 – V2 tPat2 = c2 tJoe2
tPat2 (c2 – V2) = c2 tJoe2
tPat2 (c2 – V2)/c2 = tJoe2
tPat2 (1 – V2/c2) = tJoe2
tPat (1 – V2/c2)½ = tJoe
tPat = (1 – V2/c2)-½ tJoe
tPat = γ tJoe, where γ = (1 – V2/c2)-½
What ship speed V gives γ = 2?
2 = (1 – V2/c2)-½
2 (1 – V2/c2)½ = 1
4 (1 – V2/c2)= 1
1 – V2/c2 = ¼
1 – ¼ = V2/c2
0.75 = V2/c2
0.75½ = V/c
0.866 c = V
So if the ship moves at 86.6% the speed of light, γ will be 2.