If they [the stars] are suns having the same nature as our sun, why do not these suns collectively outdistance our sun in brilliance? Why do they all together transmit so dim a light…? When sunlight bursts into a sealed room through a hole made with a tiny pin point, it outshines the fixed stars at once. The difference is practically infinite.
So said Johannes Kepler, responding in 1610 to Galileo’s just-published Starry Messenger. Kepler was arguing against Giordano Bruno’s idea that stars were other suns, orbited by other Earths. Kepler felt that Galileo’s telescopic observations of stars strengthened the case against Bruno.
Kepler’s comments regarding the relative brightnesses of sun and stars are really perceptive. He knew what he was talking about. His comments illustrate something about the sun and stars that we probably do not appreciate.
Modern astronomers measure the brightness of stars using the “magnitude” system. The modern system is tied to an ancient rating scale for stars. On that ancient scale, the stars in the night sky that appear to be the largest (“magnitude” means “bigness”) were ranked 1; they were “stars of the 1st magnitude” (in other words, “1st-class stars”). Next came somewhat lesser stars, “stars of the 2nd magnitude” (“2nd-class stars”). And so it went, on down to those stars that were barely visible even to keen eyes under dark skies; such stars were ranked 6.
In the 19th century, astronomers figured out that the apparent sizes of stars were illusions, and that what mattered with the stars was their light output as seen from Earth—their apparent brightnesses. Astronomers developed a mathematical system for precisely stating a star’s brightness, and they tied this system to the old magnitude scale. Thus a star that ranked among the stars of the 1st magnitude in the old scale came up about a 1.0 on the new scale. The difference between a magnitude 6.0 star and a magnitude 1.0 star was a factor of 100 in brightness; 5 steps in magnitude equals a factor of 100 in brightness. In other words, a single magnitude 1.0 star lights up the night sky as much as 100 magnitude 6.0 stars.
But Sirius is actually brighter than all the other stars. If a dim star you can barely see is a 6.0, and a pretty bright star is a 2.0, and a bright star is a 1.0, then what is Sirius, which is brighter still? It turns out that in the modern magnitude system Sirius is a -1.5.
The sun, in this system, comes in at -26.7. Thus the sun is 25 steps of magnitude brighter than Sirius. Since 5 steps corresponds to a factor of 100 in brightness, and since 25 is 5 sets of 5 magnitude steps (5+5+5+5+5), then the sun is brighter than Sirius by a factor of 100×100×100×100×100. It would require 100×100×100×100×100 = 10,000,000,000 Siriuses in the night sky to be as bright as the sun. That’s 10 billion Siriuses. For reference, we can only see a few thousand stars with the naked eye, and all of them are dimmer than Sirius.
Now let’s check out what Kepler was saying about a pin-hole. Imagine you are in a dark room, like he says. Imagine the room has a high ceiling, perhaps 3 meters (roughly 10 feet) over your head. No light enters the room except through a hole in the ceiling, through which the sun shines in on you.
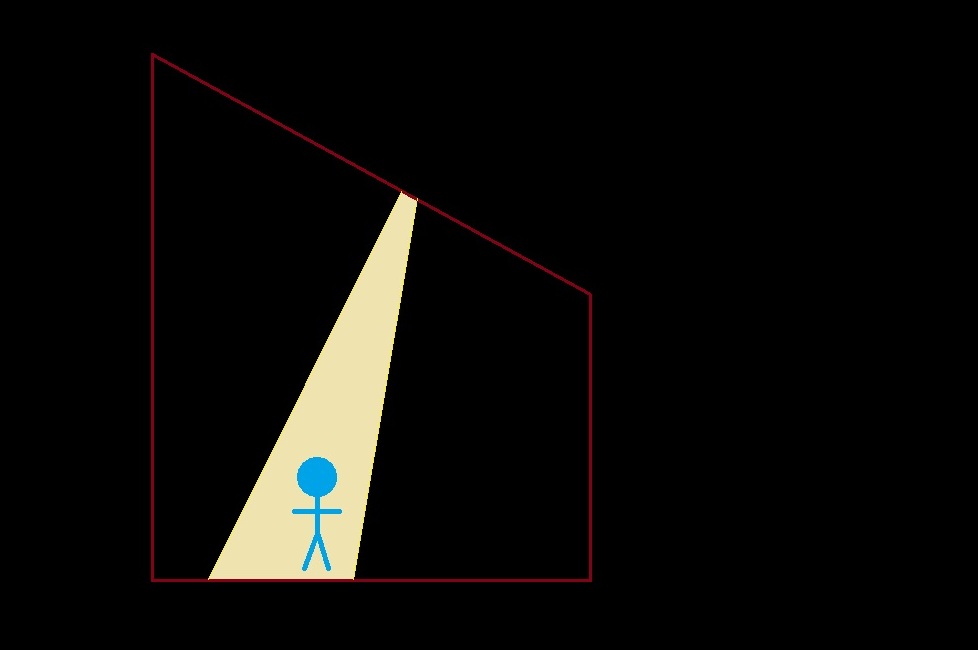
If the hole is large enough, you see the entire sun through the hole, as in the figure directly below. Thus you get the light from the full sun. But if the hole is small enough—smaller than 26 mm, or just over an inch*—then you will only see a portion of the sun, and only receive a portion of its light, as in the second figure below. In it the hole is only about a fifth the apparent diameter of the sun.
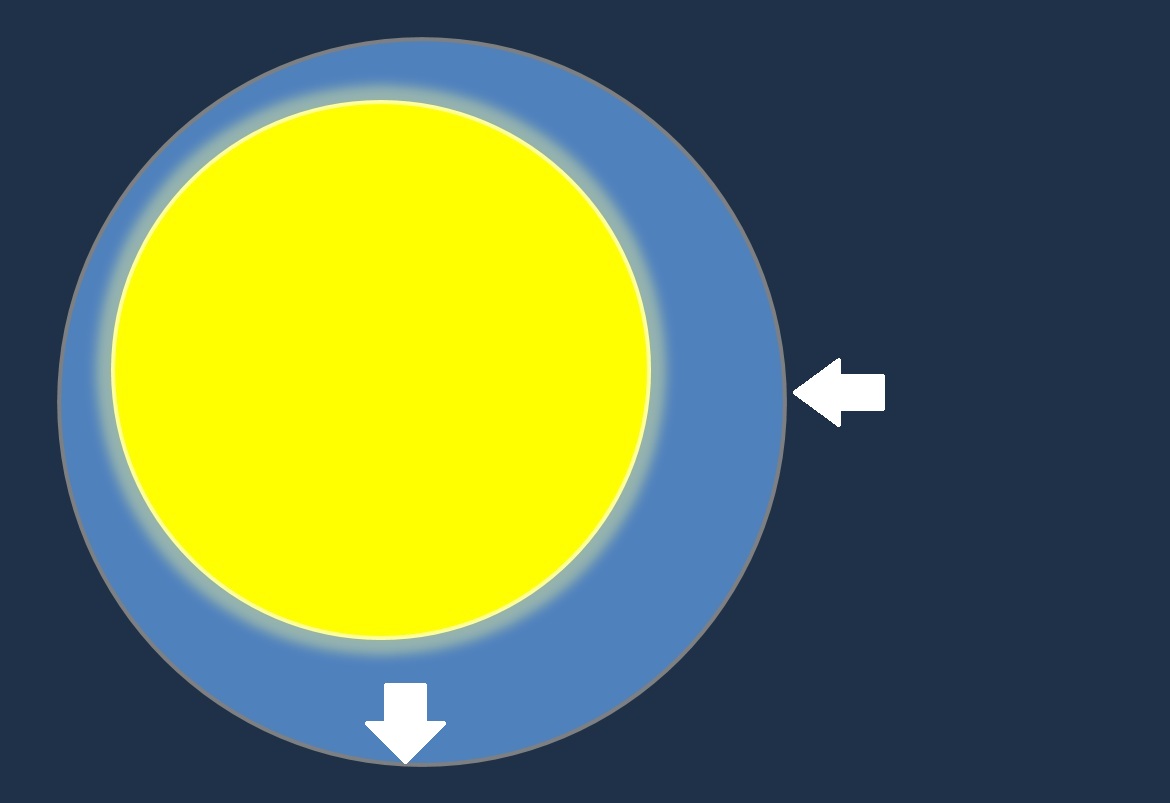The sun as seen through the hole in the ceiling if the hole is fairly large. The dark blue is the ceiling. The white arrows indicate the edge of the hole. The light blue is the sky.
The sun as seen through the hole in the ceiling if the hole is only about a fifth the apparent diameter of the sun. Here the ceiling is shown as semi-transparent so you can see the size and position of the whole sun.Area of a circle goes as diameter squared (A=πd2/4), so only (1/5)2, or 1/25th, of the sun’s area is visible through the hole. Given that the entire disk of the sun is 10 billion Siriuses, what is seen through the hole is (1/25)×10,000,000,000 = 400,000,000 or 400 million Siriuses.
Now let’s imagine a small hole, like Kepler said. Let’s imagine a hole in the ceiling that is just 1 millimeter in diameter.
A very small hole in the ceiling (arrowed).That 1 mm hole is 1/26th the diameter of the sun. Its area is (1/26)2, or 1/676th that of the sun. So the light coming through is (1/676)×10,000,000,000 = 14,800,000 or 14.8 million Siriuses.
And what if we went smaller still? How about 0.1 mm? That is really small, and would look like nothing in a high ceiling! Well, the hole would be 1/260th the diameter of the sun. Its area would be (1/260)2, or 1/67,600th of the sun, letting through the light of 148,000 Siriuses! Remember that the difference between a bright star in the night sky and the faintest stars visible is only a factor of 100; this is a factor of 148,000. This 0.1 mm hole would be a blazing beacon compared to Sirius—exactly as Kepler said.
Even if you imagine the hole being 0.01 mm (how you would make a hole so small in any real ceiling, I am not sure) it would still blaze with the light of 1,480 Siriuses—still overpowering Sirius more than bright stars in the night sky outshine the faintest stars visible.
So Kepler was right. There is an immense difference between the sun and the stars. Kepler estimated that the size a star appears to the naked eye was about the size the 1 mm hole appeared in the example above. That is also about the size that most other astronomers had estimated, too, from Ptolemy in ancient times down to Tycho Brahe (Kepler’s former boss) at the end of the 16th century, and it is the size that most people today will estimate for bright stars, if they have not already learned that star sizes are illusory. The 1 mm hole was the one that equaled 14.8 million Siriuses, so the sun wildly overpowers the stars, not just as a whole, but also size for size.
Kepler did not understand the illusory nature of star sizes at the time—no one really did—so his overall analysis was flawed. However, in terms of the appearance of stars and the sun he was absolutely correct. They do not look like they could be the same kind of body. And that’s why he thought Bruno’s claims were so ridiculous.
*The sun’s apparent diameter is half a degree. The size of hole needed to just see the entire sun through a ceiling 3 meters overhead would be a half degree portion of a circle 3 m in radius. The circumference of a circle is C = 2πr. The fraction of the full 360 degree circumference needed for a half degree hole is (0.5/360) × 2πr, or, for our ceiling, (0.5/360) × 2π × 3 m = 0.0262 meters, or 26.2 mm.
