- Books (two)
- 94 pages; 70 pages
- Level: university
George Berkeley’s 1734 The Analyst; or, A Discourse Addressed to an Infidel Mathematician criticizes how mathematicians thought regarding the “Method of Fluxions” (in modern terms, “Calculus”) of Isaac Newton, especially when some of those mathematicians were “infidels” (atheists) who criticized theological thought. Thus the title page of The Analyst quotes the Book of Matthew: “First cast out the beam out of thine own Eye; and then shalt thou see clearly to cast out the mote out of thy brother’s eye [7:5, KJV].”
Berkeley, a bishop in the Church of Ireland, acknowledges that Fluxions is “the general Key, by help whereof the modern Mathematicians unlock the secrets of Geometry, and consequently of Nature…. [and] that which hath enabled them so remarkably to outgo the Ancients in discovering Theorems and solving Problems….” However, Fluxions relies on concepts of infinity, applied repeatedly, and “to conceive a Quantity infinitely small… is, I confess, above my Capacity. But to conceive a Part of such infinitely small Quantity, that shall be still infinitely less than it… is, I suspect, an infinite Difficulty to any Man whatsoever….”
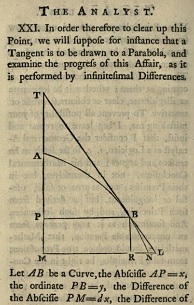
A major point of Berkeley’s is the idea of a second or third or fourth fluxion—called today a second, third, or fourth derivative. A derivative is a slope at some certain point—a point being infinitesimal in nature. Berkeley raises the conceptual problem of a slope within that slope, and then within that, and so on? Such things, he says, are nevertheless accepted by the same people who demand rigorous evidence in theology, and who claim to only believe what evidence they can see:
He who can digest a second or third Fluxion, a second or third Difference, need not, methinks, be squeamish about any Point in Divinity…. [W]ith what appearance of Reason shall any Man presume to say, that Mysteries may not be Objects of Faith, at the same time that he himself admits such obscure Mysteries to be the Object of Science?
Thus Berkeley argues that atheist mathematicians, who are so particular about points of religion, are more lax about their own field, submitting to authority, taking things on trust, and believing things that cannot be seen and mysteries that cannot be conceived. They have obstructions in their own eyes that they should look to cast out.
Berkeley’s 1735 A Defence of Free-Thinking in Mathematics responds to criticism of The Analyst. Berkeley emphasizes his interest in Truth, as he sees it, as opposed to the interest in Authority of the Infidel/atheist Mathematician. He asserts that the issue is not whether the “Method of Fluxions” is functionally useful, but whether the concepts in it are conceivable and solid, or whether mathematicians essentially accept it on faith based in its usefulness and in the reputation of Newton. Berkeley writes:
There are too many that deride Mysteries, and yet admire Fluxions; who yield that Faith to a mere Mortal, which they deny to Jesus Christ, whose Religion they make it their Study and Business to discredit…. I endeavour to shew, that such Men are defective in Point of Reason and Judgment, and that they do the very Thing they would seem to despise.
Stephen Mason, in his 1962 A History of the Sciences, credits Berkeley’s work with stimulating British mathematicians to inquire into the logical foundations of Calculus, and to place it upon a more secure foundation.
Click here to read The Analyst, courtesy of Archive.org.
Click here to read a 1901 re-publication of The Analyst, courtesy of Google Books.
Click here to read Defence, courtesy of Erara.
Click here to read a 1901 re-publication of Defence, courtesy of Google Books.