Go outside on a summer night, look up at the sky, and observe the stars. Some stars are bright, like Vega and Arcturus. Some are middling, like Polaris (the North Star) and Mizar (the star in the “bend” of the Big Dipper’s handle). Some are dim, like Rho Leo (in the constellation of Leo, the lion) and Alcor (the faint companion of Mizar). When we look at these stars, what are we seeing? How do we know what the stars are? We hear that the sun is a star; are the stars of the summer sky suns?
We learn about stars through their light. That is all we see from them, as even powerful telescopes struggle to reveal the bodies of stars. Last week we got to know the magnitude system, which is based on a star’s light. The modern magnitude system is a way of quantifying how bright stars seem to the eye. It is based on the light intensity from a star, the light power per unit area (Watts per square centimeter or W/cm2) that reaches our eyes. A change of five steps on the magnitude scale corresponds to a factor of 100 in intensity. The light that reaches our eye from a first magnitude star has 100 times the intensity of the light that reaches our eye from a sixth magnitude star.
Some of the stars of the summer sky as represented by the Stellarium planetarium app.To know more about the stars, we need to consider what things might affect the intensity of light reaching Earth from a star. These are pretty basic: the distance of the star, and its power output or luminosity. Obviously the farther away a star is, the weaker in intensity its light will be when it reaches Earth and the less bright the star will appear. And obviously a less powerful star will appear less bright than a more powerful star at the same distance.
The gray/black sphere is twice the radius of the blue sphere, and has four times the surface area.The relationship between distance and brightness is pretty simple. As light travels away from a star, it spreads out in all directions, like an expanding sphere. The surface area of a sphere is determined by the square of the sphere’s radius. Increase the distance to a star by a factor of 2, and you increase the surface area over which the light is spread by a factor of 2×2=4. Thus you decrease the intensity of the star’s light by a factor of 4, too. Increase the distance by a factor of 10, and you increase the area the light is spread over by a factor of 10×10=100, and you decrease the intensity of the star’s light by a factor of 100.
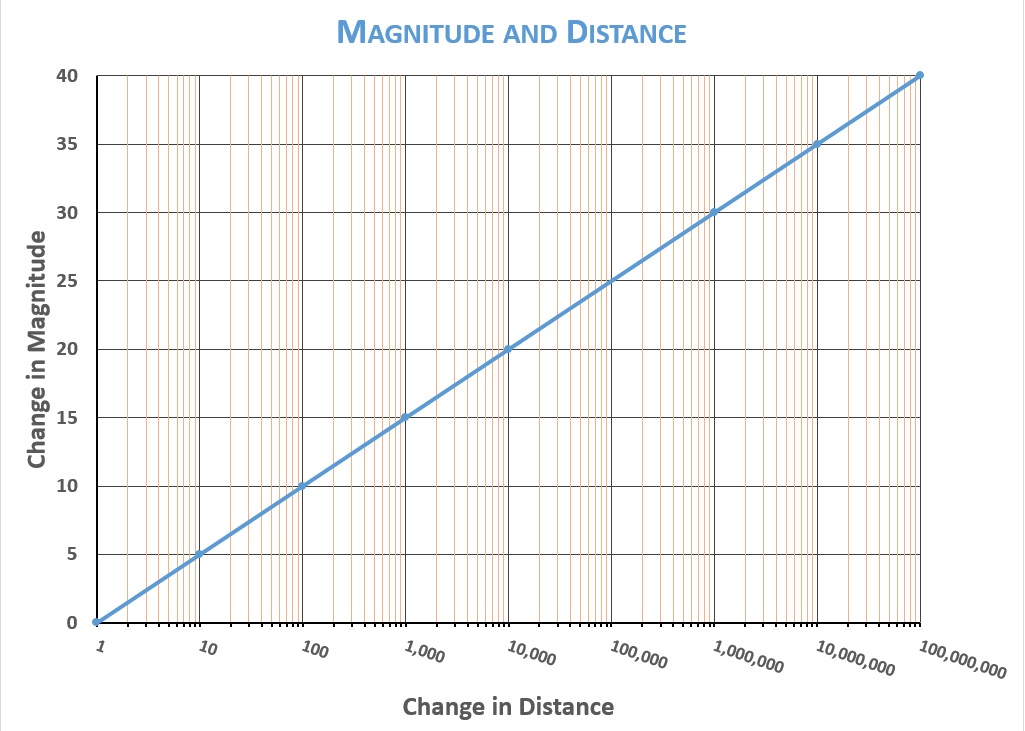
But a change in intensity by a factor of 100 is a change of five steps on the magnitude scale. The star Spica is a summer sky star whose magnitude is about 1.0. A star identical to Spica but ten times farther away from Earth would be five magnitudes fainter—magnitude 6.0. Were it a hundred times farther from Earth, it would be magnitude 11.0 (too faint for the eye to see, but detectable by telescopes). The graph below shows the relationship between distance and magnitude:
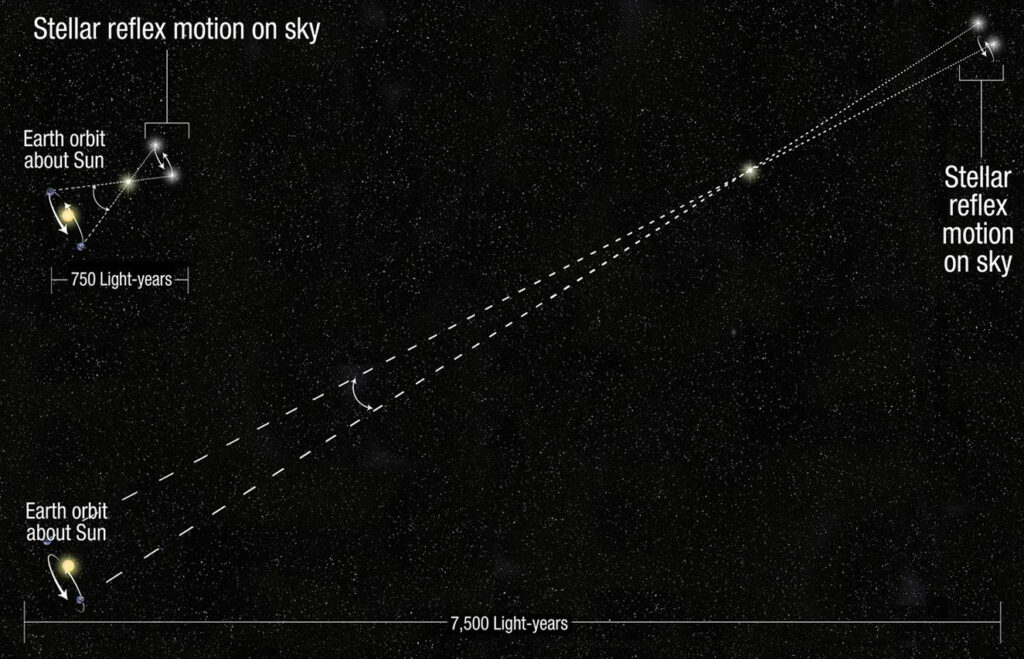
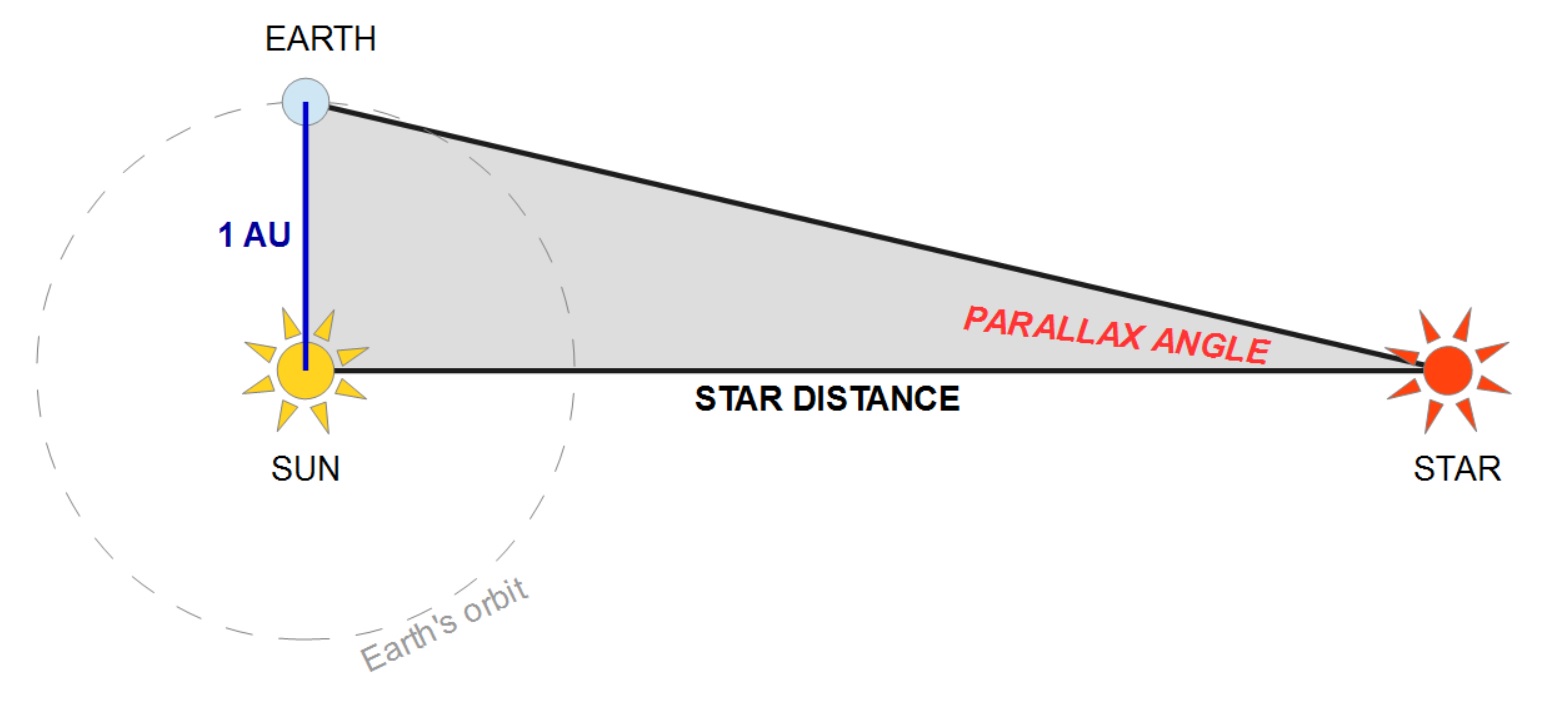
How can we determine the distance to a star? Through the parallax angle created by Earth’s motion about the sun, as illustrated below.
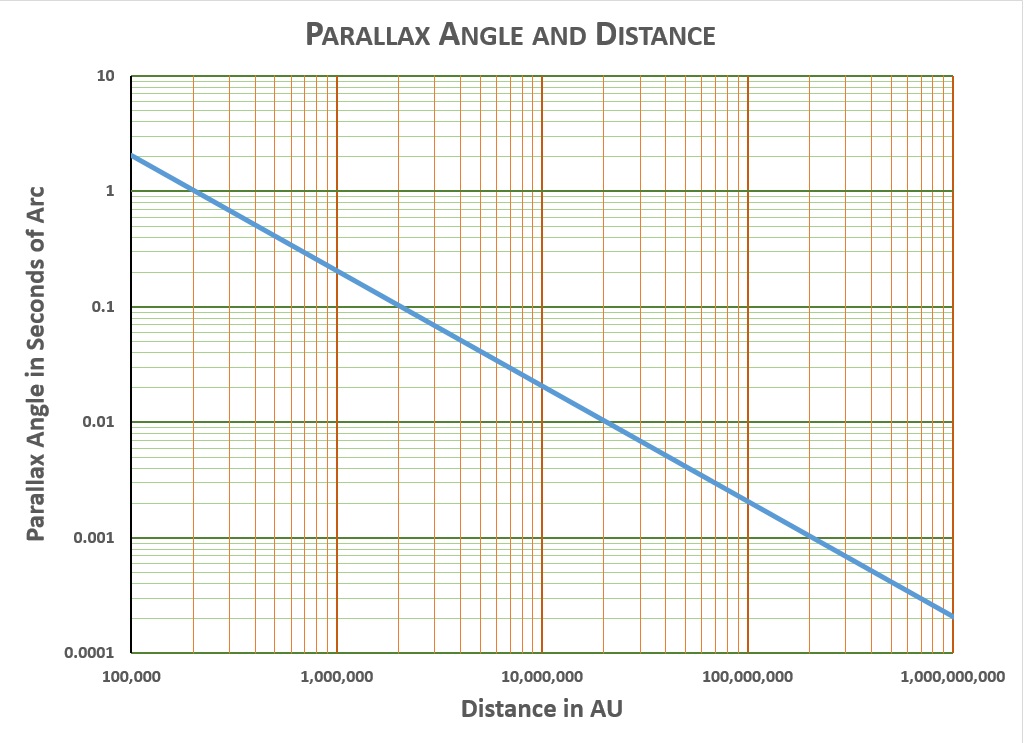
The closer the star, the larger the parallax angle, which is usually measured in seconds of arc (just like there are 3600 seconds of time in an hour—60 seconds per minute times 60 minutes per hour—there are 3600 seconds of arc in a degree). The Earth-to-sun distance is one Astronomical Unit, or AU. This chart shows the relationship between distance in AU and parallax angle in seconds of arc:*
Luminosity is a little more complex of an issue than distance, because luminosity itself depends on a star’s temperature and size. Temperature has the bigger effect. As discussed in a previous post, stars give off light in the same way as, and produce the same continuous ROYGBIV rainbow spectrum as, a piece of glowing hot iron or any piece of glowing hot, dense, incandescent material. So we suppose that the star and the iron have much in common. The proportion of colors in the rainbow emitted by an incandescent body depends upon temperature—the hotter a piece of iron (or a star) is, the more it radiates blue and violet light versus red and orange light. Thus as an incandescent body’s temperature rises its color changes from glowing dull red, to glowing orange-yellow, then white, and then even blue-white. The color of an incandescent body then indicates its temperature. The sun is a yellow star. Stars that are redder in color are cooler than the sun. The coolest, reddest stars are only about half as hot as the sun. On the other hand, the hottest, bluest stars are more than twice as hot as the sun.
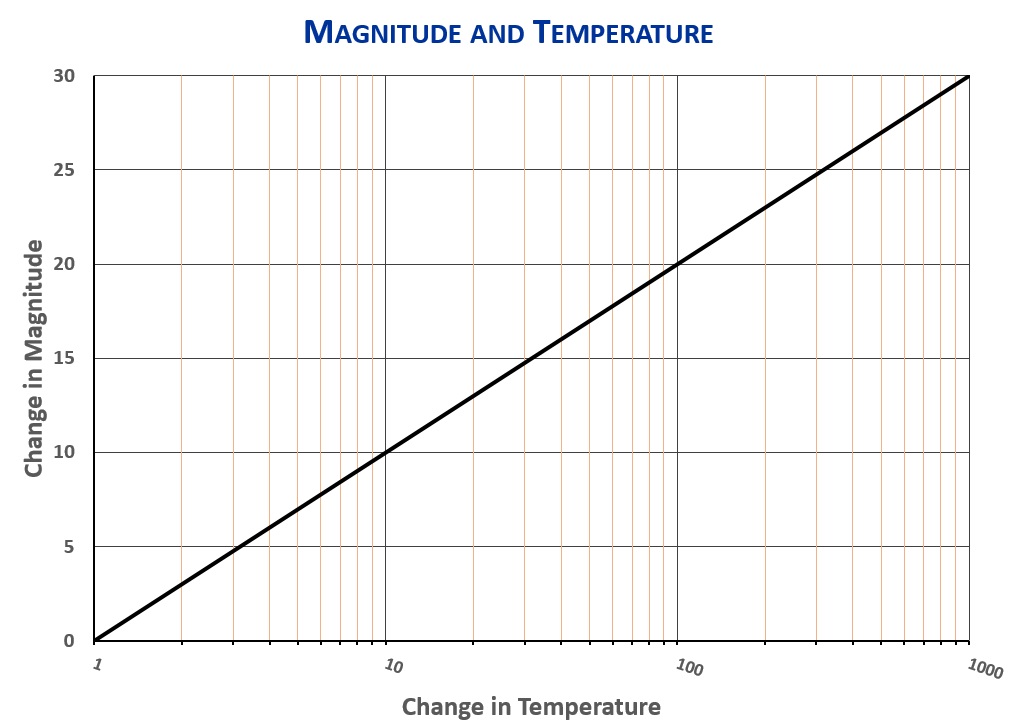
Not only does the color of light emitted by an incandescent body change with temperature, but the quantity of light changes, too. A piece of iron that is glowing orange-yellow is more luminous than if it is only red hot. This effect is tremendous. Luminosity—the “wattage” of light emitted—goes as the fourth power of temperature, meaning that a star that is twice the temperature of Spica (but the same size) will have 2x2x2x2=16 times Spica’s luminosity! A star the same size as Spica but one tenth as hot would be 10x10x10x10=10,000 times less luminous. Since 10,000 is two factors of 100 (100×100=10,000), and since a change of 100 corresponds to five steps on the magnitude scale, a star one tenth as hot as Spica would be 10 steps down on the magnitude scale, at magnitude 11.0. The relationship between temperature and magnitude is shown here:
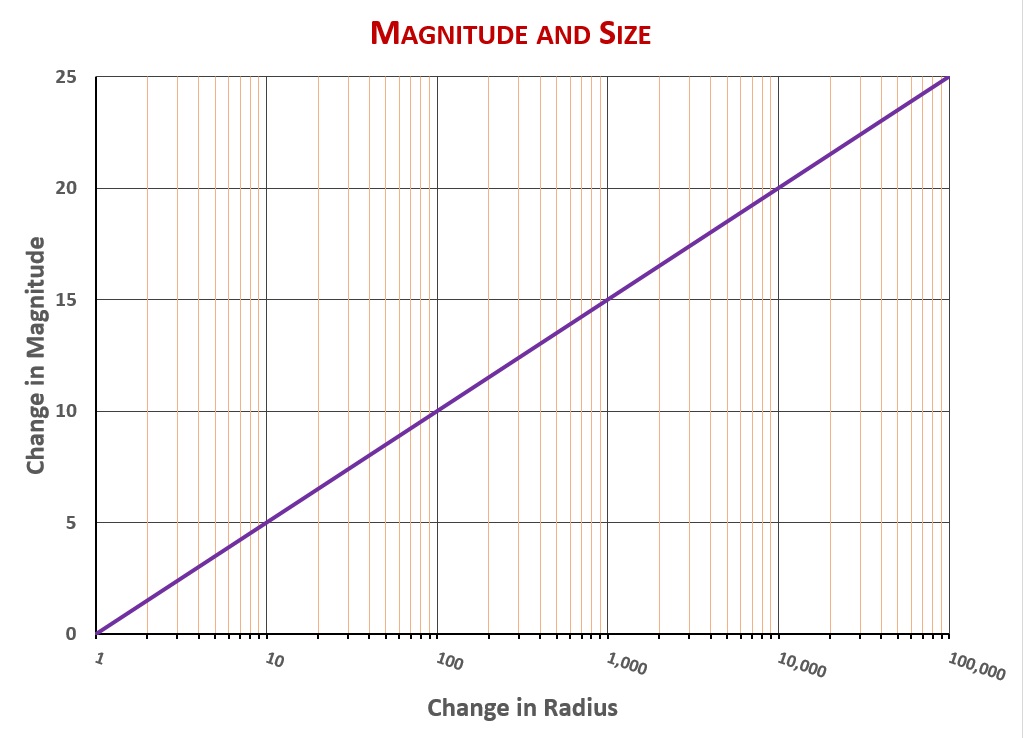
Size has a lesser effect on luminosity than temperature. Luminosity follows the surface area of a star, and since surface area of a sphere goes as the square of radius, a star twice the radius of Spica (but the same temperature) would have 2×2=4 times the luminosity. A star one tenth the radius of Spica (but the same temperature and the same distance from Earth), would be 10×10=100 times less luminous—and thus five steps down from Spica on the magnitude scale, at magnitude 6.0. Here is a graph of the relationship between size and magnitude:
We now have everything we need to figure out what these stars we see really are. That is next week’s topic.
*For those who want the math of the parallax-and-distance chart: For the small angles involved in parallax the relationship between parallax and distance is simple:
PARALLAX ANGLE = EARTH-to-SUN DISTANCE / STAR DISTANCE
In terms of AU, this is
PARALLAX ANGLE = 1 AU / STAR DISTANCE IN AU
This formula gives the parallax angle in radian units. There are 57.3 degrees in a radian, and 3600 seconds of arc in a degree, so to get this formula to work in seconds of arc it needs to have those correction factors built in
PARALLAX ANGLE = (1 AU / STAR DISTANCE IN AU) x 3600 x 57.3
This last formula is what is plotted on the chart.
